線性代數是數學的分支學科，涉及矢量、矩陣和線性變換。

它是機器學習的重要基礎，從描述算法操作的符號到代碼中算法的實現，都屬于該學科的研究范圍。

雖然線性代數是機器學習領域不可或缺的一部分，但二者的緊密關系往往無法解釋，或只能用抽象概念（如向量空間或特定矩陣運算）解釋。

閱讀這篇文章后，你將會了解到：

如何在處理數據時使用線性代數結構，如表格數據集和圖像。

數據準備過程中用到的線性代數概念，例如 one-hot 編碼和降維。

深度學習、自然語言處理和推薦系統等子領域中線性代數符號和方法的深入使用。

讓我們開始吧。

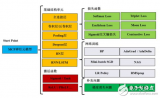
這 10 個機器學習案例分別是：

Dataset and Data Files 數據集和數據文件

Images and Photographs 圖像和照片

One-Hot Encoding one-hot 編碼

Linear Regression 線性回歸

Regularization 正則化

Principal Component Analysis 主成分分析

Singular-Value Decomposition 奇異值分解

Latent Semantic Analysis 潛在語義分析

Recommender Systems 推薦系統

Deep Learning 深度學習

1. 數據集和數據文件

在機器學習中，你可以在數據集上擬合一個模型。

這是表格式的一組數字，其中每行代表一組觀察值，每列代表觀測的一個特征。

例如，下面這組數據是鳶尾花數據集的一部分

5.1，3.5，1.4，0.2，Iris-setosa

4.9，3.0，1.4，0.2，Iris-setosa

4.7，3.2，1.3，0.2，Iris-setosa

4.6，3.1，1.5，0.2，Iris-setosa

5.0，3.6，1.4，0.2，Iris-setosa

這些數據實際上是一個矩陣：線性代數中的一個關鍵數據結構。

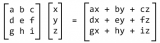
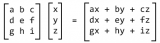
接下來，將數據分解為輸入數據和輸出數據，來擬合一個監督機器學習模型（如測量值和花卉品種），得到矩陣（X）和矢量（y）。矢量是線性代數中的另一個關鍵數據結構。

每行長度相同，即每行的數據個數相同，因此我們可以說數據是矢量化的。這些行數據可以一次性或成批地提供給模型，并且可以預先配置模型，以得到固定寬度的行數據。

2. 圖像和照片

也許你更習慣于在計算機視覺應用中處理圖像或照片。

你使用的每個圖像本身都是一個固定寬度和高度的表格結構，每個單元格有用于表示黑白圖像的 1 個像素值或表示彩色圖像的 3 個像素值。

照片也是線性代數矩陣的一種。

與圖像相關的操作，如裁剪、縮放、剪切等，都是使用線性代數的符號和運算來描述的。

3. one-hot 編碼

有時機器學習中要用到分類數據。

可能是用于解決分類問題的類別標簽，也可能是分類輸入變量。

對分類變量進行編碼以使它們更易于使用并通過某些技術進行學習是很常見的。one-hot 編碼是一種常見的分類變量編碼。

one-hot 編碼可以理解為：創建一個表格，用列表示每個類別，用行表示數據集中每個例子。在列中為給定行的分類值添加一個檢查或「1」值，并將「0」值添加到所有其他列。

例如，共計 3 行的顏色變量：

red

green

blue

。。.

這些變量可能被編碼為：

red， green， blue 1， 0， 0 0， 1， 0 0， 0， 1 。。.

每一行都被編碼為一個二進制矢量，一個被賦予「0」或「1」值的矢量。這是一個稀疏表征的例子，線性代數的一個完整子域。

4. 線性回歸

線性回歸是一種用于描述變量之間關系的統計學傳統方法。

該方法通常在機器學習中用于預測較簡單的回歸問題的數值。

描述和解決線性回歸問題有很多種方法，即找到一組系數，用這些系數與每個輸入變量相乘并將結果相加，得出最佳的輸出變量預測。

如果您使用過機器學習工具或機器學習庫，解決線性回歸問題的最常用方法是通過最小二乘優化，這一方法是使用線性回歸的矩陣分解方法解決的（例如 LU 分解或奇異值分解）。

即使是線性回歸方程的常用總結方法也使用線性代數符號：

y = A 。 b

其中，y 是輸出變量，A 是數據集，b 是模型系數。

5. 正則化

在應用機器學習時，我們往往尋求最簡單可行的模型來發揮解決問題的最佳技能。

較簡單的模型通常更擅長從具體示例泛化到未見過的數據。

在涉及系數的許多方法中，例如回歸方法和人工神經網絡，較簡單的模型通常具有較小的系數值。

一種常用于模型在數據擬合時盡量減小系數值的技術稱為正則化，常見的實現包括正則化的 L2 和 L1 形式。

這兩種正則化形式實際上是系數矢量的大小或長度的度量，是直接脫胎于名為矢量范數的線性代數方法。

6. 主成分分析

通常，數據集有許多列，列數可能達到數十、數百、數千或更多。

對具有許多特征的數據進行建模具有一定的挑戰性。而且，從包含不相關特征的數據構建的模型通常不如用最相關的數據訓練的模型。

我們很難知道數據的哪些特征是相關的，而哪些特征又不相關。

自動減少數據集列數的方法稱為降維，其中也許最流行的方法是主成分分析法（簡稱 PCA）。

該方法在機器學習中，為可視化和模型創建高維數據的投影。

PCA 方法的核心是線性代數的矩陣分解方法，可能會用到特征分解，更廣義的實現可以使用奇異值分解（SVD）。

7. 奇異值分解

另一種流行的降維方法是奇異值分解方法，簡稱 SVD。

如上所述，正如該方法名稱所示，它是源自線性代數領域的矩陣分解方法。

該方法在線性代數中有廣泛的用途，可直接應用于特征選擇、可視化、降噪等方面。

在機器學習中我們會看到以下兩個使用 SVD 的情況。

8. 潛在語義分析

在用于處理文本數據的機器學習子領域（稱為自然語言處理），通常將文檔表示為詞出現的大矩陣。

例如，矩陣的列可以是詞匯表中的已知詞，行可以是文本的句子、段落、頁面或文檔，矩陣中的單元格標記為單詞出現的次數或頻率。

這是文本的稀疏矩陣表示。矩陣分解方法（如奇異值分解）可以應用于此稀疏矩陣，該分解方法可以提煉出矩陣表示中相關性最強的部分。以這種方式處理的文檔比較容易用來比較、查詢，并作為監督機器學習模型的基礎。

這種形式的數據準備稱為潛在語義分析（簡稱 LSA），也稱為潛在語義索引（LSI）。

9. 推薦系統

涉及產品推薦的預測建模問題被稱為推薦系統，這是機器學習的一個子領域。

例如，基于你在亞馬遜上的購買記錄和與你類似的客戶的購買記錄向你推薦書籍，或根據你或與你相似的用戶在 Netflix 上的觀看歷史向你推薦電影或電視節目。

推薦系統的開發主要涉及線性代數方法。一個簡單的例子就是使用歐式距離或點積之類的距離度量來計算稀疏顧客行為向量之間的相似度。

像奇異值分解這樣的矩陣分解方法在推薦系統中被廣泛使用，以提取項目和用戶數據的有用部分，以備查詢、檢索及比較。

10. 深度學習

人工神經網絡是一種非線性機器學習算法，它受大腦中信息處理元素的啟發，其有效性已經在一系列問題中得到驗證，其中最重要的是預測建模。

深度學習是近期出現的、使用最新方法和更快硬件的人工神經網絡的復興，這一方法使得在非常大的數據集上開發和訓練更大更深的（更多層）網絡成為可能。深度學習方法通常會在機器翻譯、照片字幕、語音識別等一系列具有挑戰性的領域取得最新成果。

神經網絡的執行涉及線性代數數據結構的相乘和相加。如果擴展到多個維度，深度學習方法可以處理向量、矩陣，甚至輸入和系數的張量，此處的張量是一個兩維以上的矩陣。

線性代數是描述深度學習方法的核心，它通過矩陣表示法來實現深度學習方法，例如 Google 的 TensorFlow Python 庫，其名稱中包含「tensor」一詞。