來源:機器之心編譯 作者:Eric Jang
不確定性是機器學習領域內一個重要的研究主題,Eric Jang近日的一篇博客對這一主題進行了詳細的闡述。順便一提,他的博客還有一些有趣的深度學習迷因。
在談到人工智能安全、風險管理、投資組合優化、科學測量和保險時,人們都會提到「不確定性(uncertainty)」的概念。下面有幾個人們言語中涉及不確定性的例子:
「我們想讓機器學習模型知道它們不知道的東西。」
「負責診斷病人和給出治療方案的AI應該告訴我們它對自己的推薦的信心。」
「科學計算中的顯著性值代表了測量中的不確定性。」
「我們想讓自動智能體探索它們不確定(對于獎勵或預測)的區域,這樣它們也許能發現稀疏的獎勵。」
「在投資組合優化中,我們希望最大化回報,同時限制風險。」
「由于地緣政治不確定性增大,美國股市2018年在失望中收尾。」
那「不確定性」究竟是什么?
不確定性度量反映的是一個隨機變量的離散程度(dispersion)。換句話說,這是一個標量,反應了一個隨機變量有多「隨機」。在金融領域,這通常被稱為「風險」。
不確定性不是某種單一形式,因為衡量離散程度的方法有很多:標準差、方差、風險值(VaR)和熵都是合適的度量。但是,要記住一點:單個標量數值不能描繪「隨機性」的整體圖景,因為這需要傳遞整個隨機變量本身才行!
盡管如此,為了優化和比較,將隨機性壓縮成單個數值仍然是有用的。總之要記住,「越高的不確定性」往往被視為「更糟糕」(除了在模擬強化學習實驗中)。
不確定性的類型
統計機器學習關注的是模型p(θ|D)的估計,進而又估計的是未知隨機變量p(y|x)。其中有多種不同形式的不確定性。某些不確定性的概念描述了我們能夠預期的固有的隨機性(比如拋硬幣的結果),另一些概念則描述了我們對模型參數的最佳猜測的信心缺乏程度。
為了說得具體一點,我們假設有一個循環神經網絡(RNN)需要根據一個每日氣壓表讀數序列預測當天的降雨量。氣壓表能檢測大氣壓,大氣壓下降往往是降雨的前兆。下圖總結了降雨量預測模型與不同類型的不確定性。
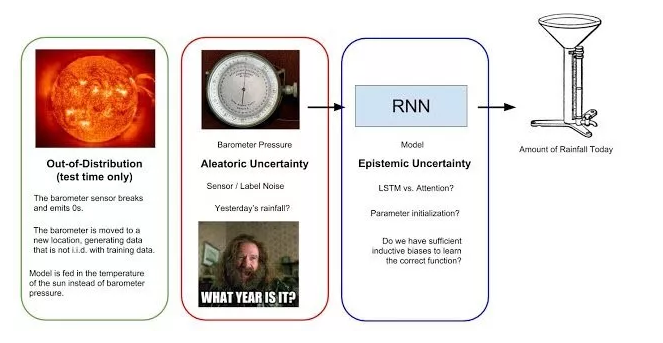
圖1:試圖根據氣壓表讀數序列預測每日降雨量的簡單機器學習模型可能考慮的不確定性。偶然事件不確定性(AleatoricUncertainty)源自數據收集過程,是不可降低的隨機性。認知不確定性(EpistemicUncertainty)反映的是模型做出正確預測的置信程度。最后,超出分布的誤差(Out-of-Distributionerror)是指當模型的輸入不同于其訓練數據時出現的不確定性(比如太陽溫度等其它異常現象)。
偶然事件不確定性
偶然事件不確定性得名于拉丁語詞根aleatorius,意為「將幾率納入創造過程」。這描述的是源自數據生成過程本身的隨機性;不能簡單地通過收集更多數據而消除的噪聲。就像你不能預知結果的拋硬幣。
在降雨量預測的類比中,偶然事件不確定性源自氣壓表的不準確度。也還存在這種數據收集方法沒有觀察的重要變量:昨日的降雨量是多少?我們測量大氣壓的時代是現代還是上個冰河時代?這些未知是我們的數據收集方法中固有的,所以用該系統收集更多數據無法幫助我們消除這一不確定性。
偶然事件不確定性會從輸入傳播到模型的預測結果。假設有一個簡單模型y=5x,它的輸入取自正態分布x~N(0,1)。在這一案例中,y~N(0,5),因此該預測分布的偶然事件不確定性可描述為σ=5。當然,當輸入數據x的隨機結構未知時,預測結果的偶然事件不確定性將更難估計。
也許有人會想:因為偶然事件不確定性是不可約減的,所以我們對此無能無力,直接忽略它就好了。這可不行!在訓練模型時,應該注意選擇能夠正確地代表偶然事件不確定性的輸出表征。標準的LSTM不會得出概率分布,所以學習拋硬幣的結果時只會收斂成均值。相對而言,用于語言生成的模型能夠得出一系列類別分布(詞或字符),這能納入句子完成任務中的固有歧義性。
認知不確定性
「好的模型都是相似的;差的模型各有不同。」
認知不確定性來自希臘語詞根epistēmē,屬于與知識相關的知識。這衡量了我們對「源自我們對正確模型參數的無知程度」的正確預測的無知程度。
下圖展示了一個在某個簡單的一維數據集上的高斯過程回歸模型。其置信區間反映了認知不確定性;訓練數據的認知不確定性為零(紅點)。隨著我們離訓練數據點的距離越遠,模型應該給預測分布分配越高的標準差。不同于偶然事件不確定性,認知不確定性可以通過收集更多數據和「去除」模型缺乏知識的輸入區域而降低。
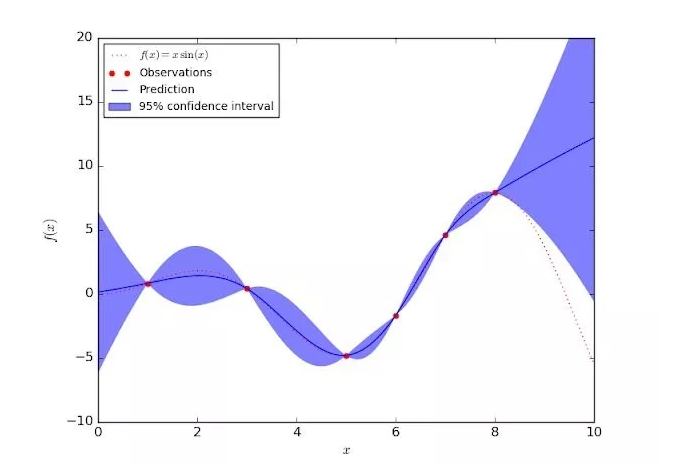
圖2:一維高斯過程回歸模型,展現了訓練集之外的輸入上的認知不確定性
深度學習與高斯過程之間有豐富的關聯。人們希望能通過神經網絡的表征能力擴展高斯過程的能感知不確定性的性質。不幸的是,高斯過程難以擴展用于大數據集的統一隨機小批量設置,而且研究大型模型和數據集的人也已經不再支持這種方法。
如果人們希望在選擇模型族時有最大的靈活度,使用集成(ensemble)方法來估計不確定性是一個好選擇,這實際上就是使用「多個獨立的學習后的模型」。高斯過程模型是分析式地定義預測分布,而集成方法則被用于計算預測的經驗分布(empiricaldistribution)。
由于訓練過程中出現的隨機化偏差,任何單個模型都會有一些誤差。在集成方法中,其它模型往往會揭示出單個模型特有的錯處之處,同時認同推理正確的預測結果;因此集成模型是很強大的。
我們該如何隨機取樣模型以構建一個集成模型呢?在使用bootstrapaggregation構建集成模型時,我們首先從一個大小為N的訓練數據集開始,并從原始訓練集采樣M個大小為N的數據(有替換,這樣每個數據集都不會占據整個數據集)。分別在這些數據集上訓練M個模型,再將它們的預測結果綜合起來得到一個經驗預測分布。
如果訓練多個模型的成本過高,也可以使用dropout訓練來近似模型集成。但是,引入dropout會涉及到一個額外的超參數并且也可能有損單個模型的表現(對于實際應用而言往往是不可接受的;在實際應用中,校準不確定性估計相對準確度而言是次要的)。
因此,如果能使用大量計算資源(就像谷歌那樣),通常只需要重復訓練多個模型副本,這要更加容易。這還能在無損性能的前提下享受集成方法的好處。這篇深度集成論文就采用了這一方法:https://arxiv.org/pdf/1612.01474.pdf。這篇論文的作者還提到由不同的權重初始化帶來的隨機訓練動態足以得到一個多樣化的模型集合,而不必通過bootstrapaggregation來降低訓練集多樣性。從實際的工程開發角度看,押注不會影響模型性能的風險估計方法或研究者想要嘗試的其它方法是明智的
超出分布的不確定性
對于我們的降雨量預測器,如果我們為其提供的輸入不是氣壓表讀數序列,而是太陽的溫度呢?要是提供一個全是零的序列呢?或者用不同的單位記錄的氣壓表讀數呢?RNN還是會繼續計算,為我們提供一個預測,但結果很可能毫無意義。
這個模型完全沒有能力基于通過不同于訓練集創建流程的流程生成的數據進行預測。在基準驅動的機器學習研究領域,這是一種常被忽視的失敗模式,因為我們通常假設訓練、驗證和測試集都完全由獨立同分布的數據構成。
確定輸入是否「有效」是實際部署機器學習所面臨的一個嚴峻問題,這也被稱為超出分布(OoD/OutofDistribution)問題。OoD與「模型誤設錯誤」和「異常檢測」是同義詞。
異常檢測不僅對增強機器學習系統穩健性很重要,而且本身也是一種非常有用的技術。舉個例子,我們可能想構建一個能監控健康人士的生命體征的系統,讓該系統能在指標異常時發出警報,這并不需要系統之前見過這種異常的病理模式。我們也可以用異常檢測來管理數據中心的「健康」,一旦有不同尋常的事情發生(磁盤滿載、安全漏洞、硬件故障等),我們就能得到通知。
因為OoD輸入僅出現在測試時間,所以我們不應假設我們事先知道模型會遇到的異常的分布。這正是OoD檢測的棘手之處——我們必須針對模型在訓練階段從未見過的輸入來增強該模型對這些輸入的抗性!這正是對抗式機器學習中描述的標準的攻擊場景。
機器學習模型有兩種處理OoD輸入的方法:1)在輸入到達模型前就識別出糟糕的輸入;2)根據模型預測結果的「怪異性」來幫助我們鑒別可能存在問題的輸入。
在第一種方法中,我們不會對下游機器學習任務做任何假設,只會考慮輸入是否處于訓練分布中的問題。這正是生成對抗網絡(GAN)中判別器的工作。但是,單個判別器并不具有完美的穩健性,因為它只擅長辨別真實數據分布和生成器得到的分布;對于不屬于其中任意一個分布的輸入而言,它有可能得出任意的預測結果。
除了判別器,我們也可以構建一個分布內數據的密度模型,比如一個核密度估計器或用一個NormalizingFlow來擬合數據。HyunsunChoi和我最近研究過這一問題,參閱我們最近使用現代生成模型執行OoD檢測的論文:https://arxiv.org/abs/1810.01392
第二種OoD檢測方法涉及到使用任務模型的預測(認知)不確定性來辨別哪些輸入是OoD。理想情況下,模型在收到錯誤的輸入時應該會得到「怪異的」的預測分布p(y|x)。舉個例子,HendrycksandGimpel(https://arxiv.org/abs/1610.02136)表明OoD輸入的最大化softmax概率(預測得到的類別)往往低于分布內的輸入。這里,不確定性反比于最大softmax概率建模的「置信度」。高斯過程這樣的模型能通過構造為我們提供這些不確定性估計,或者我們也可通過深度集成來計算認知不確定性。
在強化學習領域,人們實際上假設OoD輸入是一件好事,因為這是智能體還不知道如何處理的世界輸入。鼓勵策略尋找自己的OoD輸入能實現「內在的好奇心」,從而探索模型的預測效果較差的區域。這是很好的做法,但我很好奇如果將這種好奇心驅動的智能體部署到現實世界(其中傳感器很容易損壞,也會發生其它實驗異常)中會怎樣。機器人如何區分「未曾見過的狀態」(好)和「傳感器損壞情況」(壞)?這能得到能學習與它們的傳感機制交互從而生成最大化新穎度的智能體嗎?
誰來看住看門狗?
正如前一節提到的那樣,保護自己免受OoD輸入影響的一種方法是設置一個能夠「像看門狗一樣」監控模型輸入的似然模型(likelihoodmodel)。我更喜歡這種方法,因為這能將OoD輸入問題與任務模型中的認知和偶然事件不確定性隔開。從工程開發角度看,這能讓分析工作更輕松。
但我們不應該忘記這個似然模型也是一個函數近似器,可能存在自己的OoD錯誤!我們近期的生成式集成方法(GenerativeEnsembles,https://arxiv.org/abs/1810.01392,也可參閱DeepMind的同期研究https://arxiv.org/abs/1810.09136)研究表明,在使用一個CIFAR似然模型時,來自SVHN的自然圖像實際上比CIFAR分布內的圖像本身還有更高的可能性!
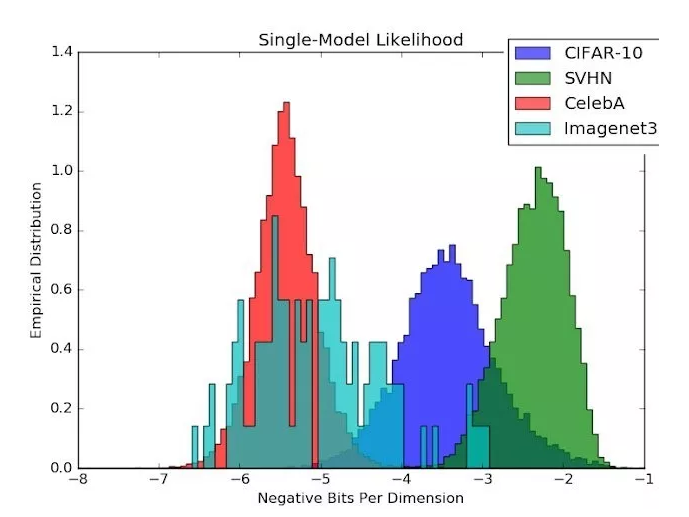
圖3:似然估計涉及到一個本身也可能易受OoD輸入影響的函數近似器。比起CIFAR測試圖像,CIFAR的似然模型會給SVHN圖像分配更高的概率!
但是,希望還是有的!研究表明,似然模型的認知不確定性對該似然模型自身而言是出色的OoD檢測器。通過將認知不確定性估計與密度估計結合起來,我們能以一種與模型無關的方式使用似然模型的集成來保護機器學習模型免受OoD輸入影響。
校準:下一件大事?
警告:只是因為一個模型能夠確定一個預測結果的置信區間,并不意味著該置信區間能真正反映結果在現實中的實際概率!
置信區間(比如2σ)隱式地假設預測分布是高斯分布,但如果你想要預測的分布是多模態分布或重尾分布,那么你的模型將不會得到很好的校準!
假設我們的降雨量預測RNN告訴我們今日的降雨將為N(4,1)英寸,如果我們的模型經過校準,那么如果我們一次又一次地在同樣的條件下重復這個實驗(也許每一次都重新訓練該模型),那么我們實際將會觀察到實際的降雨量分布正是N(4,1)。
當今學術界開發的機器學習模型大都是針對測試準確度或某個擬合度函數優化的。研究者執行模型選擇的方式不是通過重復相同的實驗來部署模型,再衡量校準誤差,所以不出意外,我們的模型往往只有很差的校準,參閱:https://arxiv.org/abs/1706.04599
展望未來,如果我們要信任部署在現實世界中的機器學習系統(機器人、醫療系統等),我認為「證明我們的模型能夠正確理解世界」的一種遠遠更為強大方法是針對統計校準測試它們。優良的校準也意味著優良的準確度,所以這是一個更嚴格的更高的優化指標。
不確定性應該是標量嗎?
盡管標量的不確定性很有用,但它們的信息量永遠不及它們所描述的隨機變量,我發現粒子濾波和分布式強化學習等方法非常酷,因為它們是在整個分布上運行的算法,讓我們無需借助簡單的正態分布來跟蹤不確定性。除了使用單標量的「不確定性」來塑造基于機器學習的決策,現在我們也可以在決定要做什么時查詢分布的整體結構。
Dabneyetal.的ImplicitQuantileNetworks論文(https://arxiv.org/pdf/1806.06923.pdf)很好地討論了如何基于回報的分布構建「風險敏感型智能體」。在某些環境中,人們可能更偏好傾向于探索未知的機會主義策略;而在另一些環境中,未知事物可能并不安全,應當避開。風險度量的選擇本質上決定了如何將回報的分布映射成一個標量數量,然后再根據這個量進行優化。所有的風險度量都可以根據分布計算得到,所以預測整個分布能讓我們將多個風險定義輕松地組合起來。此外,支持靈活的預測分布似乎也是一個提升模型校準的好方法。
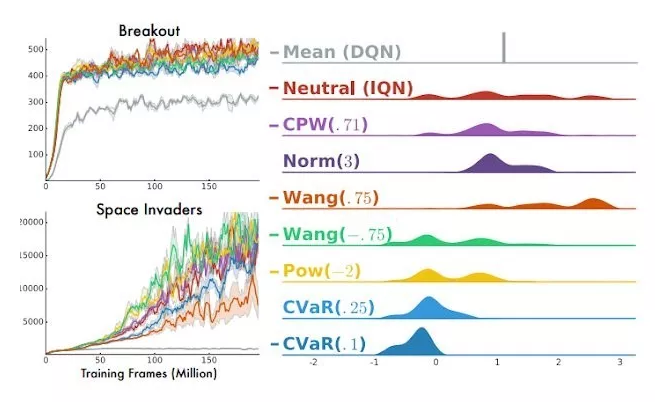
圖4:多種風險度量在Atari游戲上的表現,來自這篇IQN論文:https://arxiv.org/abs/1806.06923
對金融資產管理者而言,風險度量是一個非常重要的研究主題。簡單純粹的馬科維茨(Markowitz)投資組合的目標是最小化投資組合回報的一個加權的方差。但是,方差是「風險」在金融語境的一個不直觀的選擇:大多數投資者根本不在乎回報超出預期,而只是希望最小化回報少或虧損的可能性。由于這個原因,Value-at-Risk、ShortfallProbability和TargetSemivariance等僅關注「糟糕」結果的概率的風險度量是更有用的優化目標。
不幸的是,它們也更難分析。我希望在分布式強化學習、蒙特卡洛方法和靈活的生成模型上的研究能讓我們構建起能與投資組合優化器很好地協同工作的風險度量的可微分弛豫(differentiablerelaxations)。如果你在金融行業工作,我強烈建議你閱讀IQN論文中的「強化學習中的風險」一節。
總結
下面總結了本文的一些要點:
不確定性/風險度量是「隨機性」的標量度量。為了優化和數學計算的方便,將隨機變量濃縮成了單個數值。
預測不確定性可以分解成偶然事件不確定性(來自數據收集過程的不可約減的噪聲)、認知不確定性(對真實模型的無知)和超出分布的不確定性(在測試時,輸入存在問題)。
認知不確定性可以通過softmax預測閾值設置或集成方法降低。
我們可以不將OoD不確定性傳播到預測中,而是使用一種與任務無關的過濾機制來濾除「有問題的輸入」。
密度模型是在測試時過濾輸入的一個好選擇。但是,需要認識到,密度模型只是真實密度函數的近似,本身也可能易受分布之外的輸入的影響。
自我插拔:生成式集成方法能降低似然模型的認知不確定性,所以它們可被用于檢測OoD輸入。
校準很重要,而且在研究模型中被低估了。
某些算法(分布式強化學習)能將機器學習算法延展成能產出靈活分布的模型,這能比單個風險度量提供更多的信息。
 電子發燒友App
電子發燒友App






















評論