摘要：差分跳頻是一種數(shù)字通信系統(tǒng)，其頻率跳變速度快，通信保密性好。接收機(jī)采用軟件無(wú)線電的技術(shù)解調(diào)。解調(diào)窗口的同步是關(guān)鍵技術(shù)，是正確解調(diào)的前提。推導(dǎo)出同步算法的計(jì)算公式，給出相應(yīng)的數(shù)據(jù)圖表和流程圖。該算法同步建立時(shí)間短，運(yùn)算量小，并且可以實(shí)時(shí)調(diào)整，在仿真中取得成功。

1 差分跳頻簡(jiǎn)介

差分跳頻系統(tǒng)工作于短波波段（2MHz～30MHz），頻率跳變速度5000跳/s，最高數(shù)據(jù)傳輸速度為19.2kbps。5000跳/s的頻率跳變使得頻率不易被跟蹤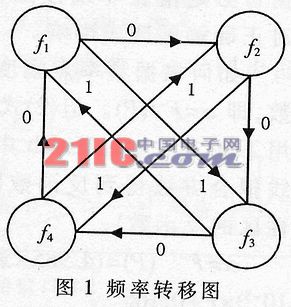，通信保密性好。差分跳頻不同于傳統(tǒng)的模擬跳頻，發(fā)射機(jī)采用DDS直接合成發(fā)送頻率，接收機(jī)采用軟件無(wú)線電方法解調(diào)。

簡(jiǎn)單說(shuō)明系統(tǒng)的工作方式，見(jiàn)圖1頻率轉(zhuǎn)移圖。系統(tǒng)待發(fā)數(shù)據(jù)為0110110……。當(dāng)?shù)谝粋€(gè)bit'0'到來(lái)時(shí)，頻率點(diǎn)由f1轉(zhuǎn)移到f2，該bit'0'用頻率f2發(fā)送；當(dāng)?shù)诙€(gè)bit'1'到來(lái)時(shí)，頻率點(diǎn)由f2轉(zhuǎn)移到f4，以此類(lèi)推解調(diào)時(shí)，將接收信號(hào)采樣的數(shù)字信號(hào)，對(duì)采樣數(shù)據(jù)進(jìn)行快速傅立葉變換（FFT）運(yùn)算，識(shí)別當(dāng)前的頻率點(diǎn)，然后保護(hù)頻率轉(zhuǎn)移圖和前一次的頻率點(diǎn)解調(diào)原始數(shù)據(jù)。

實(shí)際系統(tǒng)的參數(shù)如下：將2.56MHz～28.16MHz的頻帶等間隔劃分為10個(gè)信道，每個(gè)信道以5kHz等間隔取256頻率點(diǎn)。通信開(kāi)始前，系統(tǒng)掃描10信道，動(dòng)態(tài)決定一個(gè)特性最好的信道用來(lái)通信，收發(fā)雙方按協(xié)議從選定信道的256個(gè)頻率點(diǎn)中取64作為工作頻率，按存儲(chǔ)在系統(tǒng)中的頻率轉(zhuǎn)移圖進(jìn)行通信。該系統(tǒng)支持三種數(shù)據(jù)傳輸速率：4.8kbps、9.6kbps和19.6kbps。

2 同步策略

差分跳頻系統(tǒng)采用軟件無(wú)線電的方法進(jìn)行數(shù)據(jù)解調(diào)。軟件無(wú)線電結(jié)構(gòu)降低了系統(tǒng)硬件的復(fù)雜性，接收機(jī)不需要傳統(tǒng)模擬跳頻系統(tǒng)中的頻率合成電路和硬件的同步電路。但沒(méi)有硬件的同步電路后，采用何種軟件算法快速實(shí)現(xiàn)同步成為關(guān)鍵技術(shù)之一。

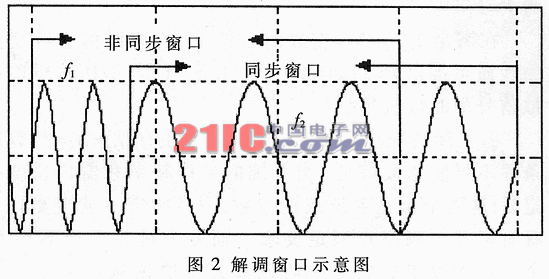
    如圖2所示，接收信號(hào)經(jīng)過(guò)A/D采樣變?yōu)閿?shù)字信號(hào)，然后對(duì)一跳時(shí)間內(nèi)（以下稱為解調(diào)窗口）的采樣數(shù)據(jù)進(jìn)行FFT運(yùn)算，識(shí)別當(dāng)前的頻率點(diǎn)，依據(jù)頻率轉(zhuǎn)移圖和前一次的頻率點(diǎn)解調(diào)原始數(shù)據(jù)。如果解調(diào)窗口不同步，則窗口內(nèi)會(huì)出現(xiàn)兩個(gè)頻率點(diǎn)，無(wú)法判定該用哪個(gè)工作為解調(diào)頻率點(diǎn)。因此必須將不同步的解調(diào)窗口滑動(dòng)到同步位置，才能正確解調(diào)數(shù)據(jù)。

筆者設(shè)計(jì)的同步方法簡(jiǎn)述如下：

（1）隨機(jī)選擇初始窗口，對(duì)采樣數(shù)據(jù)作FFT運(yùn)算，識(shí)別可能出現(xiàn)的兩個(gè)頻率點(diǎn)f1和f2以及FFT后的相應(yīng)幅度P1和P2（在頻域中頻率點(diǎn)的能量與幅度的平方成正比，為簡(jiǎn)化以幅度代替能量計(jì)算）。

（2）判斷這兩個(gè)頻率點(diǎn)在時(shí)域波形上的順序。

    （3）頻率點(diǎn)f的幅度P（請(qǐng)注意，這里指FFT后的頻域幅度）只與兩個(gè)因素有關(guān)：采樣前模擬信號(hào)的時(shí)域振幅和該頻率點(diǎn)在解調(diào)窗口內(nèi)點(diǎn)據(jù)的時(shí)間長(zhǎng)度。模擬信號(hào)的時(shí)域振幅可以在接收端采用自動(dòng)增益控制保持常數(shù)值。那么，P只要頻率點(diǎn)在解調(diào)窗口內(nèi)點(diǎn)據(jù)時(shí)間長(zhǎng)度（也就是該頻率點(diǎn)占據(jù)的采樣點(diǎn)數(shù)目）的單值函數(shù)，只要找到這個(gè)函數(shù)，即可先由FFT計(jì)算出幅度P，反求該頻率點(diǎn)占據(jù)的窗口長(zhǎng)度，最后將窗口滑動(dòng)適當(dāng)長(zhǎng)度即可同步。

以下假設(shè)：采樣頻率為fs,解調(diào)窗口總長(zhǎng)度為N，某一頻率點(diǎn)占據(jù)的長(zhǎng)度為N1。

定義：α=N1/N

3 實(shí)現(xiàn)的方式

具體實(shí)現(xiàn)要考慮很多復(fù)雜的情況，詳細(xì)說(shuō)明如下。

首先要找到（3）中提及的函數(shù)關(guān)系，這個(gè)函數(shù)關(guān)系記為P=F(α)。

在滿足（f1/fs）×N1=整數(shù)的條件下，由離散傅立葉變換的性質(zhì)可推出P=F（α）=A·（N/4）·α，A是A/D采樣前模擬信號(hào)的時(shí)域振幅。

但實(shí)際情況更為復(fù)雜。上面提到的（f1fs）×N1=整數(shù)的條件不可能總被滿足。當(dāng)系統(tǒng)的采樣頻率和窗口長(zhǎng)度確定后（這兩個(gè)量是系統(tǒng)級(jí)的參數(shù)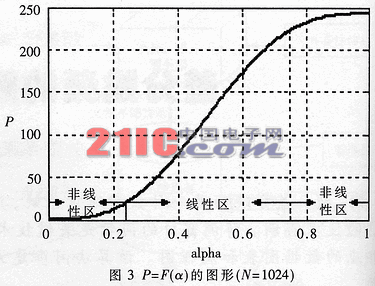，一經(jīng)確定不能變更），只有有限幾個(gè)頻率點(diǎn)滿足要求。而差分跳頻系統(tǒng)需要64個(gè)工作頻率點(diǎn)，它們是收發(fā)雙方按協(xié)議從選定信道的512個(gè)頻率點(diǎn)中選擇的，也就是說(shuō)512個(gè)頻點(diǎn)都有可能成為工作頻率點(diǎn)，絕大部分不滿足工作。如果條件得不到滿足，那么公式修改為P=F（α）=H（f, α）·A·(N/4)·α。因子H（f,α）依賴于頻率和α。H（f,α）無(wú)法動(dòng)態(tài)自適應(yīng)計(jì)算，因?yàn)橐蕾囉?alpha;，而α恰好是要求解的變量。因此，直接對(duì)采樣數(shù)據(jù)進(jìn)行計(jì)算的方法不太可取。

還有一點(diǎn)，希望該跳頻系統(tǒng)降低對(duì)同步的敏感性，從而降低復(fù)雜性和運(yùn)算量，因此希望P=F（α）是非線性函數(shù)，以改善系統(tǒng)特性。

可采用對(duì)采樣數(shù)據(jù)預(yù)先加窗函數(shù)修正的方法。本系統(tǒng)采用海明窗，因?yàn)楹Ｃ鞔笆菨M足要求的最簡(jiǎn)單窗函數(shù)，并且可以理論推導(dǎo)出P=F(α)的函數(shù)式。海明窗定義為：

W（n）=0.5+0.5cos[2(π-N/2)] n=0,1,2,…，N-1 （1）

經(jīng)過(guò)推導(dǎo)得到加窗后的P=F（α）的估計(jì)式為：

P=F（α）=0.935A·N·{α/4-sin(2πα)/(8π)+[cos(α)-1]/(8π)} (2)

圖3是用Matlab仿真得出的P=F（α）的圖形。該圖形不是按（2）式直接繪制的，它是實(shí)際仿真得到的結(jié)果，與（2）式彼此獨(dú)立，但（2）式的圖形也基本是這個(gè)圖形。（2）式中的系數(shù)0.93可以在（0.92～0.94）之間微調(diào)。

圖3是Matlab按下述方法計(jì)算得到的：對(duì)應(yīng)每一個(gè)α值，在滿足采樣定理前提下隨機(jī)選擇1000點(diǎn)頻率，讓其占據(jù)的窗口相對(duì)長(zhǎng)度為α，計(jì)算FFT后的頻域幅度，求1000點(diǎn)的平均值作為縱坐標(biāo)。因此圖3所表達(dá)的函數(shù)不依賴于具體頻率。這個(gè)圖劃分為線性區(qū)和非線性區(qū)，線性區(qū)的范圍為0.25<α<0.75。解調(diào)窗口進(jìn)入非線性區(qū)的意思是窗口位置距離同步位置非常近了，再經(jīng)過(guò)細(xì)致調(diào)整就可以同步。

圖3整體上是非線性函數(shù)，非線性的好處是降低了系統(tǒng)對(duì)同步的敏感性。假設(shè)解調(diào)窗口稍微不同步，那么窗口必定落在非線性區(qū)，在該區(qū)幅度變化不顯著，不會(huì)對(duì)正確解調(diào)造成影響。

    如果根據(jù)頻率點(diǎn)幅度P求α？先求解P=F(α)的反函數(shù)，即α=F-1（P）。但（2）式求不出閉合解析的反函數(shù)。可用下述方法：在Matlab中繪制圖3的反函數(shù)，再使用曲線擬合方法得到反函數(shù)的表達(dá)式（公式（3）只適用于線性區(qū)的反函數(shù)）：

α=F-1（P）=（4.985×10-8）×P3-(1.8×10-5) ×P2+(4.131×10-3) ×P+0.166

第二個(gè)復(fù)雜的情況是必須判斷解調(diào)窗口類(lèi)型。

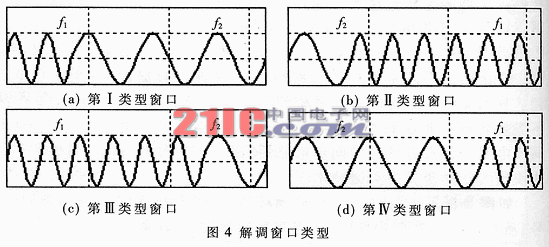
假設(shè)初始的解調(diào)窗口未同步，則該窗口內(nèi)有兩個(gè)頻率點(diǎn)f1和f2，依據(jù)這兩個(gè)頻率的時(shí)域順序和所占據(jù)的窗口長(zhǎng)度（也就是域中兩個(gè)頻率的幅度）有四種情況，分別稱為第I、第II、第III、第IV類(lèi)型窗口，見(jiàn)圖4。每個(gè)窗口都假定不同步，且只繪出一跳時(shí)間內(nèi)的波形。

為什么要判定窗口類(lèi)型呢？因?yàn)閷?shí)際計(jì)算時(shí)取幅度較大的頻率點(diǎn)來(lái)求解α，這樣可降低噪聲的干擾。但幅度較大的頻率點(diǎn)可能是f1也可能是f2，在時(shí)域中的順序可能在前也可能在后，于是形式四種類(lèi)型。

如果初始窗口進(jìn)入非線性區(qū)，因非線性區(qū)頻率點(diǎn)幅度變化小，為降低噪聲影響，在非線性區(qū)移動(dòng)的點(diǎn)就是固定值（這個(gè)值可以根據(jù)實(shí)際需要加以微調(diào)）。判斷窗口是否進(jìn)入非線性區(qū)的準(zhǔn)則為：是否有一個(gè)頻點(diǎn)的幅度超過(guò)門(mén)限值。

圖5

4 流程

經(jīng)過(guò)以上討論，得出實(shí)際的算法流程見(jiàn)圖5。

說(shuō)明：如果第一次滑動(dòng)窗口后未能進(jìn)入預(yù)定同步位置，則繼續(xù)第二次調(diào)整。此時(shí)移動(dòng)后的窗口以大概率進(jìn)入大非線性區(qū)，如果第二次滑動(dòng)窗口仍舊不同步，則繼續(xù)第三次調(diào)整，至多三次調(diào)整后，以95%概率進(jìn)入同步鎖定。三次調(diào)整后仍不同步（至多5%概率），判定為同步失敗，選擇窗口重新計(jì)算。

以上的窗口是向右滑動(dòng)的（也就是向時(shí)間軸正向滑動(dòng)），如果系統(tǒng)開(kāi)辟較大緩沖區(qū)，也可以向左滑動(dòng)（也就是向時(shí)間軸負(fù)向滑動(dòng)），此時(shí)前面的數(shù)據(jù)不能丟失，并且對(duì)第III和第IV類(lèi)型窗口的滑動(dòng)點(diǎn)數(shù)變?yōu)榻^對(duì)值較小的負(fù)數(shù)值。

該同步算法的優(yōu)點(diǎn)是同步建立時(shí)間短，運(yùn)算量小，可以實(shí)時(shí)調(diào)整。對(duì)接收數(shù)據(jù)加窗函數(shù)修正降低了系統(tǒng)對(duì)同步的敏感性。該算法在系統(tǒng)仿真中取得成功。