矢量信號分析儀是常用的進行雷達和無線通訊信號分析的儀器。

模擬掃描調諧式頻譜分析儀使用超外差技術覆蓋廣泛的頻率范圍 ; 從音頻、微波直到毫米波頻率。快速傅立葉變換 (FFT) 分析儀使用數字信號處理(DSP) 提供高分辨率的頻譜和網絡分析。如今寬帶的矢量調制 ( 又稱為復調制或數字調制 ) 的時變信號從 FFT 分析和其他 DSP 技術上受益匪淺。VSA 提供快速高分辨率的頻譜測量、解調以及高級時域分析功能，特別適用于表征復雜信號，如通信、視頻、廣播、雷達和軟件無線電應用中的脈沖、瞬時或調制信號。

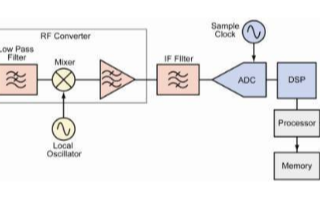
圖 1 顯示了一個簡化的 VSA 方框圖。VSA 采用了與傳統掃描分析截然不同的測量方法 ; 融入 FFT 和數字信號處理算法的數字中頻部分替代了模擬中頻部分。傳統的掃描調諧式頻譜分析是一個模擬系統 ; 而 VSA 基本上是一個使用數字數據和數學算法來進行數據分析的數字系統。VSA 軟件可以接收并分析來自許多測量前端的數字化數據，使您的故障診斷可以貫穿整個系統框圖。

圖 1. 矢量信號分析過程要求輸入信號是一個被數字化的模擬信號，然后使用 DSP 技術處理并提供數據輸出 ; FFT 算法計算出頻域結果，解調算法計算出調制和碼域結果。

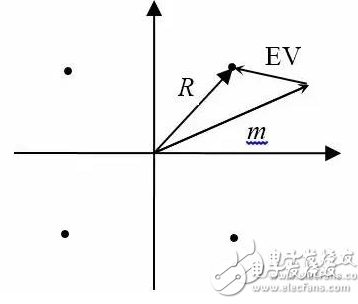
VSA 的一個重要特性是它能夠測量和處理復數數據，即幅度和相位信息。實際上，它之所以被稱為“矢量信號分析”正是因為它采集復數輸入數據，分析復數數據，并輸出包含幅度和相位信息的復數數據結果。矢量調制分析執行測量接收機的基本功能。在下一篇“矢量調制分析基礎”中，您將了解到矢量調制與檢波的概念。

在使用適當前端的情況下，VSA 可以覆蓋射頻和微波頻段，并能提供額外的調制域分析能力。這些改進可以通過數字技術來實現，例如模擬 - 數字轉換，以及包含數字中頻 (IF) 技術和快速傅立葉變換 (FFT) 分析的 DSP。

因為要分析的信號變得越來越復雜，最新一代的信號分析儀已經過渡到數字架構，并且往往具有許多矢量信號分析和調制分析的能力。有些分析儀在對信號進行放大，或進行一次或多次下變頻之后，就在儀器的輸入端數字化信號。在大部分現代分析儀中，相位連同幅度信息都被保留以進行真正的矢量測量。另一方面，其它的前端如示波器和邏輯分析儀等對整個信號進行數字化，同時也保留了相位和幅度信息。VSA 無論作為合成的測量前端的一部分，還是單獨在內部運行或在與前端相連的計算機上運行的軟件，它的分析能力都依賴于前端的處理能力，無論前端是綜合測量專用軟件，還是矢量分析測量動態信號并產生復數數據結果。

VSA 相比模擬掃描調諧分析有著獨特的優勢。一個主要的優勢是它能夠更好地測量動態信號。動態信號通常分為兩大類 : 時變信號或復數調制信號。時變信號是指在單次測量掃描過程中，被測特性發生變化的信號 ( 例如突發、門限、脈沖或瞬時信號 )。復數調制信號不能用簡單的 AM、FM 或 PM 調制單獨描述，包含了數字通信中大多數調制方案，例如正交幅度調制 (QAM)。

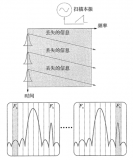
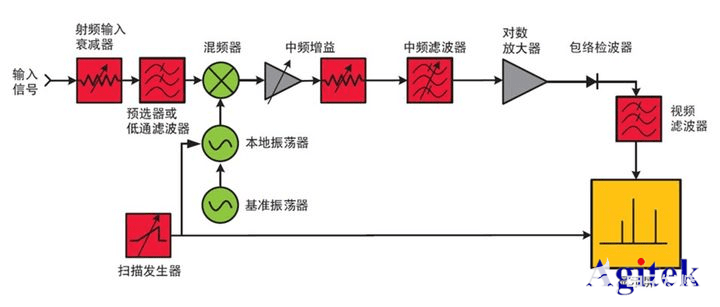
圖 2. 掃描調諧分析顯示了一個窄帶 IF 濾波器對輸入信號的瞬時響應。矢量分析使用 FFT 將大量時域采樣轉換到頻域頻譜。

傳統的掃描頻譜分析實際上是讓一個窄帶濾波器掃過一系列頻率，按順序每次測量一個頻率。對于穩定或重復信號，這種掃描輸入的方法是可行的，然而對掃描期間發生變化的信號，掃描結果就不能精確地代表信號了。

還有，這種技術只能提供標量 ( 僅有幅度 ) 信息，不過有些信號特征可以通過進一步分析頻譜測量結果推導得出。

VSA 測量過程通過信號“快照”或時間記錄，然后同時處理所有頻率，以仿真一系列并聯濾波器從而克服了掃描局限。例如，如果輸入的是瞬時信號，那么整個信號事件被捕獲 ( 意味著該時刻信號的所有信息都被捕獲和數字化 ); 然后經過 FFT 運算，得出“瞬時”復數頻譜對頻率的關系。這一過程是實時進行的，所以就不會丟失輸入信號的任何部分。基于這些，VSA 有時又稱為“動態信號分析”或“實時信號分析”。不過， VSA 跟蹤快速變化的信號的能力并不是無限制的。它取決于 VSA 所具有的計算能力。

并行處理為高分辨率 ( 窄分辨率帶寬 ) 測量帶來另一個潛在的優勢：那就是更短的測量時間。如果你曾經使用過掃描調諧頻譜分析儀，就會知道在較小小頻率掃寬下的窄分辨率帶寬 (RBW) 測量可能非常耗時。掃描調諧分析儀對逐點頻率進行掃描的速度要足夠慢以使模擬分辨率帶寬濾波器有足夠的建立時間。與之相反，VSA 可以一次性測量整個頻率掃寬。不過，由于數字濾波器和 DSP 的影響，VSA 也有類似的建立時間。與模擬濾波器相比，VSA 的掃描速度主要受限于數據采集和數字處理的時間。但是，VSA 的建立時間與模擬濾波器的建立時間相比通常是可以忽略不計的。對于某些窄帶測量，VSA 的測量速度可以比傳統的掃描調諧分析快 1000 倍。

在掃描調諧頻譜分析中，掃描濾波器的物理帶寬限制了頻率分辨率。VSA 沒有這一限制。VSA 能夠分辨間隔小于 100 μHz 的信號。VSA 的分辨率通常受限于信號和測量前端的頻率穩定度，以及在測量上希望花費的時間的限制。分辨率越高，測量信號所需要的時間 ( 獲得要求的時間記錄長度 ) 就越長。

另一個極為有用的特性是時間捕獲能力。它使你可以完整無缺地記錄下實際信號并在以后重放，以便進行各種數據分析。捕獲的信號可用于各種測量。例如，捕捉一個數字通信的發射信號，然后既進行頻譜分析也進行矢量調制分析，以測量信號質量或識別信號缺損。

使用數字信號處理 (DSP) 還帶來其它優勢；它可以同時提供時域、頻域、調制域和碼域的測量分析。集這些能力于一身的儀器更有價值，它可改善測量質量。VSA 的 FFT 分析使你可以輕松和準確地查看時域和頻域數據。DSP提供了矢量調制分析，其中包括模擬和數字調制分析。模擬解調算法可提供與調制分析儀類似的 AM、FM 和 PM 解調結果，使您可以看到幅度、頻率和相位隨時間變化的曲線圖。數字解調算法可適用于許多數字通信標準 ( 例如GSM、cdma2000®、WiMAXTM、LTE 等 ) 的廣泛的測量，并獲得許多有用的測量顯示和信號質量數據。

很明顯 VSA 提供了許多重要的優勢，當配合使用合適的前端時，還可以提供更多、更大的優勢。例如，當 VSA 與傳統的模擬掃描調諧分析儀結合使用時，可提供更高的頻率覆蓋率和更大的動態范圍測量能力 ; 與示波器結合使用時，可提供寬帶分析 ; 與邏輯分析儀結合使用時，可探測無線系統中的FPGA 和其它數字基帶模塊。

如前所述，VSA 本質上是一個數字系統，它使用 DSP 進行 FFT 頻譜分析，使用解調算法進行矢量調制分析。FFT 是一種數學算法，它對時間采樣數據提供時域－頻域的轉換。模擬信號必須在時域中被數字化，再執行 FFT 算法計算出頻譜。從概念上說，VSA 的實施是非常簡單直接的 : 捕獲數字化的輸入信號，再計算測量結果。參見圖 3。不過在實際中，必須考慮許多因素，才能獲得有意義和精確的測量結果。

圖 3. 1 kHz FFT 分析舉例 : 先數字化時域信號，再使用 FFT 將其轉換到頻域

如果你熟悉 FFT 分析，就知道 FFT 算法針對所處理的信號有幾點假設條件。算法不校驗對于所給輸入這些假設是否成立，這就有可能產生無效的結果，除非用戶或儀器可以驗證這些假設。

圖 1 為一般的 VSA 系統方框圖。在 DSP 過程中，不同的環節可能使用不同的功能。VSA 測量過程包括這些基本階段:

測量前端
1. 包括頻率轉換的信號調整。基于所使用的前端硬件，可能需要和 / 或可以使用不同的信號調整步驟。
2. 模數轉換器
3. 正交檢波
VSA 軟件
4. 數字濾波和重采樣
5. 數據窗口
6. FFT 分析 ( 對于矢量調制，由解調模塊替代模塊 5 和 6)

測量過程的第一個階段稱為信號調整。這個階段包括幾個重要的功能，對信號進行調整和優化，以便于模擬- 數字轉換和 FFT 分析。第一個功能是AC 和 DC 耦合。如果您需要移除測量裝置中無用的 DC 偏置，就必須使用這一項。接下來信號被放大或衰減，以達到混頻器輸入的最佳信號電平。混頻器階段提供信號頻率的轉換或射頻到中頻的下變頻，并將信號最后混頻為中頻。

這一操作與掃描調諧分析中的超外差功能相同，將 FFT 分析能力擴展到微波頻段。實際上，要獲得最后的中頻頻率，可能需要經過多個下變頻階段。有些信號分析儀提供外部 IF 輸入能力 ; 你可以通過提供自己的 IF，延展 VSA 的頻率上限范圍，從而與自己提供的接收機相匹配。

信號調整過程的最后階段是預防信號混疊，它對于采樣系統和 FFT 分析極為重要。抗混疊濾波執行這一功能。如果 VSA 測量沒有對混疊做出足夠的預防，那么它可能會顯示不屬于原始信號的頻率分量。采樣定律告訴我們，如果信號采樣速率大于信號中最高頻率分量的兩倍，被采樣的信號就可以被準確重建。最低的可接受的采樣率稱為奈奎斯特 (Nyquist) 采樣率。

因此，ƒs > 2 (ƒmax)
其中 ƒs = 采樣率
ƒmax = 最高頻率分量

如果違反了采樣定律，就會得到“混疊的”錯誤分量。因此，為了預防所給最大頻率出現混疊結果，在 1/2 采樣率以上不能有太大的信號能量。頻率較高的波形違反了采樣定律。

除非使用抗混疊濾波器，否則這兩個頻率在進行數字處理時將會混淆。為了預防混疊，必須滿足兩個條件 :

1. 進入數字轉換器 / 采樣器的輸入信號必須是帶限的。換句話說，必須存在一個最大頻率 (ƒmax)，沒有任何頻率分量高于這個頻率。

2. 必須以符合采樣定律的速率對輸入信號進行采樣。

解決混疊問題的方案看起來很簡單。首先選擇前端硬件將要測量的最大頻率 (ƒmax)，然后確保采樣頻率 (ƒs) 是該最大頻率的兩倍。這個步驟滿足了條件 2，并確保 SA 軟件能夠對感興趣的頻率進行精確分析。接下來插入低通濾波器 ( 抗混疊濾波器 )，以去除高于 ƒmax 的所有頻率，從而確保除了感興趣的頻率進行測量以為，其它頻率都被排除。這個步驟滿足條件 1，并確保對信號的帶寬進行了限制。

有兩個因素會導致簡單的抗混疊方法復雜化。第一個也是最容易解決的因素是，抗混疊濾波器的滾降 (roll off) 速率是有限的。如圖 6 所示，在實際濾波器的通帶和截止帶之間有一個過渡帶。這個過渡帶中的頻率可能產生混疊。為了避免這些混疊分量，濾波器的截止頻率必須低于理論頻率上限 ƒs/2 。

解決這個問題的簡單辦法是使用過采樣 ( 以高于 Nyquist 采樣率的速率進行采樣 )。使采樣頻率略高于 ƒmax 的兩倍，也就是截止帶實際開始頻率的兩倍，而不是要測量的頻率的兩倍。許多 VSA 的實現都使用保護帶以防止顯示混疊的頻率分量。FFT 計算超出 50% ƒs ( 相當于 ƒs/2) 的頻譜分量。保護帶大約在 ƒs 的40% 至 50% ( 或 ƒs/2.56 至 ƒs/2) 之間并且沒有顯示，因為它可能被混疊分量破壞。不過當 VSA 軟件進行逆 FFT 運算時，在保護帶中的信號用于提供最精確的時域結果。高滾降率濾波器再結合保護帶，會抑制潛在的混疊分量，并將它們衰減到遠低于測量前端的底噪。

另一個致使混疊預防 ( 有限的頻率分辨率 ) 復雜化的因素解決起來難得多。首先，為寬頻掃寬 ( 高采樣率 ) 設計的抗混疊濾波器不適用于測量小分辨率帶寬，原因有二個 : 一是需要極大的樣本數量 ( 內存分 )，二是需要驚人的 FFT 計算量 ( 長測量時間 )。例如，當采樣率為 10 MHz 時，一個 10 Hz 分辨率帶寬的測量將需要超過 100 萬點的 FFT，也就是需要使用巨大容量的存儲器和極長的測量時間。這是不可接受的，因為小分辨率帶寬的測量能力是 VSA 的一大優勢。

提高頻率分辨率的一個方法是減小 ƒs，但代價是降低了 FFT 的頻率上限，也就是最終分析儀的帶寬。不過，這仍不失為一個好方法，因為它允許你控制測量分辨率和頻率范圍。當采樣率降低時，抗混疊濾波器的截止頻率也必須降低，否則就會發生混疊。一種可能的解決方案是對每個掃寬提供一個抗混疊濾波器，或提供一個可選擇截止頻率的濾波器。使用模擬濾波器實現這種方案的困難很多，而且成本高昂，但是有可能通過 DSP 以數字形式添加額外的抗混疊濾波器。

圖 6. 抗混疊濾波器衰減高于 ƒs/2 的信號。屏幕上不顯示介于 40% 至 50% ƒs 之間的保護帶。

數字抽取濾波器和重采樣算法提供了頻率分辨率受限制問題的解決方法。 Agilent VSA 軟件中就使用了這種方法。數字抽取濾波器和重采樣執行必要的操作以允許改變掃寬和分辨率帶寬。數字抽取濾波器同時降低采樣率并限制信號的帶寬 ( 提供混疊預防 )。輸入數字濾波器的采樣率為 ƒs; 輸出該濾波器的采樣率為 ƒs/n，其中“n”是抽取因子，為整數值。類似的，輸入濾波器的帶寬為“BW”，輸出濾波器的帶寬為“BW/n”。許多實現過程執行二進制抽取 ( 采樣率按 1/2 的速度降低 )，這意味著采樣率按 2 的整數冪改變，即步進值為 1/(2n) (1/2、1/4、1/8......)。通過“除以 2n”得出的頻率掃寬稱為基數掃寬。由于減少了 DSP 操作，通常在基數掃寬上進行的測量比在任意掃寬上進行的測量要快。

抽取濾波器允許采樣率和掃寬以 2 的冪次改變。要獲得任意掃寬，采樣率必須是無限可調的。這由抽取濾波器之后的重采樣或插值濾波器來完成。

盡管數字重采樣濾波器在降低采樣率的同時提供了混疊的預防，模擬抗混疊濾波器仍然是必要的，因為數字重采樣濾波器本身也是一個被采樣系統，必須被防止出現混疊。模擬抗混疊濾波器運行于 ƒs 上，保護最寬頻率掃寬上的分析。在模擬濾波器之后的數字濾波器，為較窄的、用戶定義的掃寬提供抗混疊能力。

當抗混疊涉及帶限信號，并使用示波器作為 VSA 軟件前端時，還必須采取額外的預防措施。

下一個限制小分辨率帶寬分析的復雜因素來源于 FFT 算法自身的本質特性 ; FFT 實質上是一個基帶轉換。這意味著 FFT 頻率范圍從 0 Hz ( 或 DC) 開始，一直到某個最大頻率 (ƒs/2) 結束。在小頻段需要被分析的測量情況中，這可能是一個重大限制。例如，如果測量前端的采樣率為 10 MHz，頻率范圍將從 0 Hz 到 5 MHz (ƒs/2)。如果時間樣本數量 (N) 為 1024，那么頻率分辨率將為 9.8 kHz (ƒs/N)。這意味著接近 9.8 kHz 的頻率可能無法分辨。

如前所述，可以通過改變采樣率來控制頻率掃寬，但是由于掃描范圍的起始頻率是 DC，所以分辨率仍然受到限制。頻率分辨率可以任意提高，但是付出的代價是最高頻率的降低。這些限制的解決方法是帶寬選擇分析，又稱為“縮放操作”或“縮放模式”。縮放操作使您可以在保持中心頻率不變的情況下減小頻率掃寬。這點非常有用，因為你可以分析和查看遠離 0 Hz 的小頻率分量。縮放操作允許你將測量焦點放在測量前端頻率范圍內的任意頻率點處 ( 圖 7)。

縮放操作是一個數字正交混頻、數字濾波和抽取重采樣的過程。感興趣的頻率掃寬與縮放掃寬中心頻率 (ƒz) 上的復數正弦波與相混頻，從而使頻率掃寬下變頻到基帶 ; 然后針對該特定掃寬對信號進行濾波和抽取 重采樣，移除所有帶外頻率。這就是在 IF ( 或基帶 ) 上的頻帶轉換信號，有時稱為“縮放時間”或“IF 時間”。也就是說，它是信號的時域表示應為它出現在接收機的中頻帶。在本章結尾的“時域顯示”部分我們將對縮放測量做進一步討論。

圖 7. 頻帶選擇分析 ( 或縮放模式 ): (a) 被測寬帶信號，(b) 被測信號的頻譜，(c) 選擇的縮放掃

寬和中心頻率，(d) 數字 LO 頻譜 ( 位于縮放中心頻率處 )，(e) 頻率掃寬下變頻到基帶，(f) 顯
示頻譜注釋經過調整，以顯示正確的掃寬和中心頻率

樣本存儲器

數字抽取濾波器的輸出代表的是帶寬受限的數字化的模擬時域輸入信號。這個數字數據流被捕獲到樣本存儲器中 ( 圖 4)。樣本存儲器是一個循環的 FIFO ( 先進先出 ) 的緩存器，它收集單個的數據采樣，形成被稱作時間記錄的數據塊，再由 DSP 進行進一步數據處理。填充時間記錄所需的時間長度與并聯濾波器分析中的初始建立時間類似。樣本存儲器所收集的時間數據是用來產生各個測量結果 ( 無論是頻域、時域或調制域 ) 的基礎數據。

時域數據校正

為了提供更精確的數據結果，VSA 軟件通過均衡濾波器進行時間數據校正。在矢量分析中，時間數據的精度非常重要。它不僅是所有解調測量的基礎，還直接用于諸如瞬時功率隨時間變化的測量中。時間數據校正是創建接近理想的頻帶限制信號過程中的最后一步。雖然數字濾波器和重采樣算法提供了任意帶寬 ( 采樣率和掃寬 ) 的支持，但是時域校正決定信號路徑的最后通帶特性。如果模擬和數字信號路徑是理想的，那么就沒有必要進行時域校正。時域校正起均衡濾波器的作用，以補償通帶內的缺損。這些缺損來源于多處。射頻部分中的 IF 濾波器、模擬抗混疊濾波器、抽取濾波器和重采樣濾波器都會對所選掃寬內的通頻段紋波和相位非線性特性有所貢獻。

在設計均衡濾波器時，首先要基于測量前端的配置，從自校準數據中提取關于模擬信號路徑的信息。使用這些數據產生頻域校正輸出顯示結果。一旦計算出模擬校正矢量，結果將被修改以便把抽取和重采樣濾波器的影響包括在內。

最后頻率響應的計算在選定了掃寬后進行，因為它決定了抽取濾波階段的數量和重采樣率。復合的校正矢量充當適用于時間數據的數字均衡濾波器的設計基礎。

FFT 假設將要處理的信號從一個時間記錄到另一個是周期性的。但大部分信號不是按時間記錄周期重復的，兩個時間記錄之間會出現不連續。因此，這個 FFT 假設條件對大多數測量是無效的，必須假設存在不連續性。如果信號不是按時間記錄周期重復，那么 FFT 將不能準確估算頻率分量。最終的效果是產生所謂的“泄漏”現象，就是能量從單一頻率擴散到一段廣泛的頻率上。模擬掃頻調諧信號分析在掃描速度對于濾波器帶寬來說太快時將產生類似的幅度和擴散誤差。

數據窗是解決泄漏問題的一個常用方法。FFT 并不是誤差的起因，它能夠對時間記錄中的信號生成“精確”的頻譜。導致誤差的罪魁禍首是時間記錄之間的非周期性信號特性。數據窗使用窗功能修改時域數據使其變成按時間記錄為周期。實際上，它強迫波形在時間記錄的兩端變成零。這由給時間記錄乘以加權的窗函數來實現。窗對時域中的數據進行變形，以改善其在頻域中的精度。參見圖 8。

圖 8. 窗功能通過修改時域波形，減少頻域中的泄漏誤差。

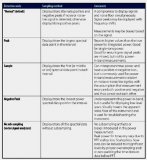
Agilent 89600B VSA 基于用戶選定的測量類型假設用戶的優先考慮情況，自動選擇適合的窗濾波器。不過，如果希望手動改變窗類型，你可以從幾種內置的窗類型中選擇。每個窗功能及其相關的 RBW 濾波器形狀擁有各自的優勢和劣勢。某窗類型可能改善了幅度精度并減少了“泄漏”，但代價卻是減小了頻率分辨率。因為每種窗類型產生不同的測量結果 ( 差異大小取決于輸入信號的特性以及觸發方式 )，所以你需要針對所進行的測量謹慎選擇適合的窗類型。表 1 總結了四種常見的窗類型及其用途。

在傳統的掃頻調諧分析中，最后的 IF 濾波器決定了分辨率帶寬。在 FFT分析中，窗類型決定了分辨率帶寬濾波形狀。窗類型和時間記錄長度決定了分辨率帶寬濾波的寬度。因此，對于給定的窗口類型，分辨率帶寬的改變將直接影響時間記錄長度。反之，時間記錄長度的改變也會導致分辨率帶寬變化，如下式所示 :
RBW = 歸一化的 ENBW/T
其中 ENBW = 等效噪聲帶寬
RBW = 分辨率帶寬
T = 時間記錄長度
等效噪聲帶寬 (ENBW) 是窗口濾波器與理想矩形濾波器進行比較的因數。它等效于通過與窗口濾波器相同數量 ( 功率 ) 白噪聲時矩形濾波器的帶寬。表1-2 列出了幾種窗類型的歸一化 ENBW 值。ENBW 等于歸一化的 ENBW 除以時間記錄長度。例如，0.5 秒時間記錄長度的漢寧窗的 ENBW 為 3 Hz (1.5 Hz-s/0.5 s)。

信號現在已經準備好進行 FFT 變換。FFT 是針對記錄以特殊方式處理采樣數據的算法。FFT 不像 ADC 轉換那樣對每個數據采樣進行處理，而是等到獲得一定數量的樣本 (N) ( 稱為時間記錄 ) 之后，再將整個數據塊進行轉換。參見圖 9。換句話說，在 FFT 中，輸入是 N 個樣本的時間記錄，輸出是 N 個樣本的頻譜。

FFT 的速度取決于對稱性或未落入限定的 2 的 N 次方的重復采樣值。FFT 分析的典型記錄長度為 1024 (210) 個采樣點。FFT 生成的頻譜在采樣頻率ƒs/2 ( 這個值稱為“折疊頻率”，ƒƒ) 兩側對稱。因此，輸出記錄的前半段包含的是冗余信息，所以只有后半段被保留，即采樣點 0 至 N/2。這表明輸出記錄的有效長度為 (N/2) + 1。必須給 N/2 加 1，因為 FFT 包含零點線，輸出從 0 Hz 至 N/2 Hz 的結果。這些都是包括幅度和相位信息的復數數據點。

理論上，FFT 算法輸出的是從 0 Hz 到 ƒ（ƒ） 范圍內的 (N/2) +1 個頻率點。不過實際中，因為需要使用預防混疊的保護帶，所以通常不是所有點都被顯示出來。如上所述，保護帶 ( 大約在 ƒs 的 40% 至 50% 之間 ) 不顯示，因為它可能被混疊分量破壞。例如，對于記錄長度為 2048 的樣本，會產生 1025 個唯一的復數頻率點，而實際上只有 801 個頻率點會被顯示出來。

圖 9. FFT 的基本關系

這些頻域點被稱為“線 (line)”或“點 (bin)”，通常編號從 0 到 N/2 。這些點相當于一組濾波器分析中的單獨的濾波器 / 檢波器輸出。點 0 包含輸入信號中的 DC 電平，稱為 DC 點。這些點在頻率上的間割是相通的，頻率步長 (Δf) 是測量時間記錄長度 (T) 的倒數，即 Δf = 1/T。時間記錄長度 (T) 由采樣率 (ƒs) 和時間記錄中的采樣點數 (N) 來確定 : T = N/ƒs。每個點的頻率 (ƒn) 如下 :

ƒn = nƒs/N
其中，n 為點數
最后一個點包含最高頻率 ƒs/2。因此 FFT 的頻率范圍從 0 Hz 到 ƒs/2。注意 FFT 最高的頻率范圍不是 FFT 算法的頻率上限 ƒmax，并且可能不同于最高的點頻率。

因為 FFT 分析在獲得至少一個時間記錄之前不能計算出有效的頻域結果，所以時間記錄長度決定了初始測量花費的時間。例如，使用 1 kHz 掃寬的 400線測量需要 400 ms 的時間記錄 ; 3200 線測量需要 3.2 s 的時間記錄。捕獲的數據時間長度與 FFT 計算引擎的處理速度無關。

在時間記錄被捕獲之后，處理速度成為一個問題。計算 FFT、調整格式和顯示數據結果所用的時間長短決定了處理的速度和顯示更新的速率。處理速度的重要性體現在兩個方面。首先，高處理速度意味著總測量時間縮
短。其次，處理速度決定了測量動態信號的能力。它的性能指標是實時帶寬(RTBW)，即在不丟失輸入信號的任何事件的情況下，可以連續處理的最大頻率掃寬。

圖 10. (a) 當 FFT 處理時間 ≤ 時間記錄長度時，處理是“實時”的；沒有數據丟失。(b) 如果

FFT 處理時間 > 時間記錄長度，那么輸入數據會丟失。

RTBW 是 FFT 處理時間等于時間記錄長度的頻率掃寬。從一個時間記錄結束到下一個時間記錄開始之間沒有間隔。參見圖 10。如果增加掃寬到超過實時帶寬，記錄長度就會變得小于 FFT 處理時間，那么時間記錄不再是連續的，有些數據將會丟失。這在 RF 測量中很常見。不過注意，時間捕獲的數據是實時的，因為所有時間樣本都直接傳輸到可用的存儲器中，而沒有數據的丟失。

VSA 允許你查看和分析時域數據。所顯示的時域數據看上去與示波器的顯示相似，但是你需要知道正在查看的數據可能是非常不同的。時域顯示的是恰好在 FFT 處理之前的時間數據。參見圖 4。 VSA 可以提供兩個測量模式 :基帶模式和縮放模式。

基于測量模式，你所看到的時域數據將有很大差別。基帶模式提供類似于你在數字示波器上看到的時間數據結果。就像傳統的數字信號示波器 (DSO)，VSA 以 0 時間和 0 Hz (DC) 為參考提供實值時間數據。

不過在 VSA 上軌跡軌跡可能出現失真，特別是在高頻情況下。這是因為 VSA 采樣率的選擇基于優化 FFT 分析，在最高頻率下每周期可能只有 2 或 3 次采樣；這對于 FFT 非常有利，但是對于觀察就不是很適合了。相反，DSO 是針對時域分析優化，對輸入通常進行過采樣。而且，DSO 可以提供額外的信號重建處理能力，使 DSO 能夠更好地顯示實際輸入信號的時域表示。此外在最大掃寬下，由于抗混疊濾波器突然的頻率截止，有些信號 ( 特別是方波和瞬時信號 ) 可能會出現過大的失真或振鈴 (ringing) 現象。從這個意義上說，DSO 適合
采樣率和時域的顯示，而不適合功率精度和動態范圍的顯示。

在縮放 ( 或頻段可選擇 ) 模式中，你觀察到的是經過混頻和正交檢波后的時間波形。特別地，所看到的時間數據是經過許多步驟處理的最后結果，基于具體的中心頻率和掃寬，這些步驟可能包括模擬下變頻、IF 濾波、數字正交混頻和數字濾波 / 重采樣。結果是一個帶寬受限的包括實部和虛部分量復數波形，并且在大多數情況下，它看起來與在示波器上的顯示不一樣。對于某些用途來說，這可能是非常有價值的信息。例如，它可以解釋為“IF 時間”，使用示波器通過在探測接收機 IF 頻段中探測而進行測量的時域信號。

數字 LO 和正交檢波算法執行縮放測量功能。在縮放測量中，所選的頻率掃寬經過下變頻到指定的中心頻率 (ƒcenter) 的基帶上。要完成它，首先數字LO 頻率被賦予 ƒcenter 值。接著輸入信號被正交檢波 ; 使用測量掃寬中心頻率的正弦和余弦 ( 正交 ) 進行相乘或混頻。結果是以 ƒcenter 為參考，相位仍與零時觸發相關的復數( 實部和虛部) 時域波形。請記住，混頻過程的結果分量是頻率的和與差( 信號 -ƒcenter 和信號+ƒcenter)。因此使用低通濾波器對數據進行進一步處理，只選擇出不同的頻率。如果載波頻率 (ƒcarrier) 等于 ƒ 中心，那么調制結果是以 0 Hz 為中點的正和負頻率邊帶。不過，頻譜顯示上的標識是正確的中心頻率和邊帶頻率值。

兩個模式測量的掃寬均為 36 MHz，起始頻率為 0 Hz。頻率點的數量設置為 401。左側時間軌跡軌跡顯示的真實周期約為 74 ns (1/13.5 MHz) 的正弦波。右側時間軌跡軌跡顯示了一個周期為 222.2 ns (1/4.5 MHz) 的正弦波。這個 4.5 MHz 正弦波是 VSA 算法中的中心頻率 18 MHz 與輸入信號 13.5 MHz 之差。

本文介紹了矢量信號分析 (VSA) 的操作理論和測量概念的入門知識。貫穿分析了整個系統方框圖，并逐一說明了每個功能以及與 FFT 測量過程的關系。你可以看到，VSA 的實現與傳統的模擬掃頻調諧信號分析有很大差異。VSA 基本上是一個包含全數字 IF、DSP 和 FFT 分析的數字系統，它提供時域、頻域、調制域和碼域信號分析能力的測試與測量解決方案。