信道最直觀的理解就是傳輸媒介，如電纜，天線，等信號傳輸的通道。

實際上，信號通常要經過以下的處理，因此又可將信道繼續劃分：

信號失真：由傅里葉變換可知，

一個信號是由不同頻率分量的信號組成的。如果不同的頻率分量的信號衰減一一致，延時也一致的話，是不會發生失真的。但如果衰減不一致，或者延時不一致的話，就會發生變形。

信道的幅頻特性和相頻特性是一條直線，則信號通過信道不會失真；

但實際上，信道的幅頻特性和相頻特性都不會是一條直線，這是信號通過信道就會產生失真；如下圖：

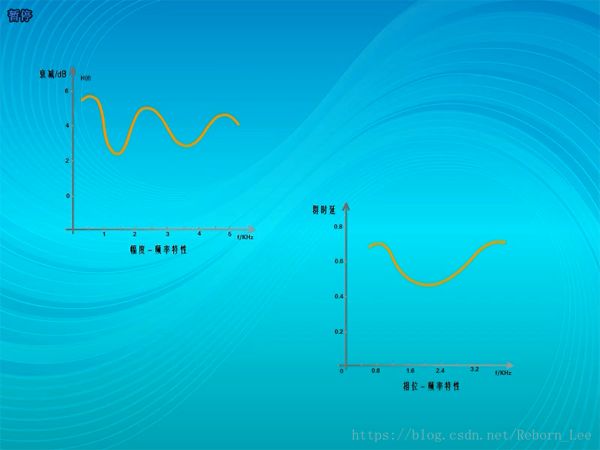
如果遇到不平坦的信道怎么辦？

幾乎沒有哪個信道的特性是平坦的，對于有線信道這種有固定的幅頻特性和相頻特性的信道可以添加一個補償電路，

使得信道特性趨于一條直線；

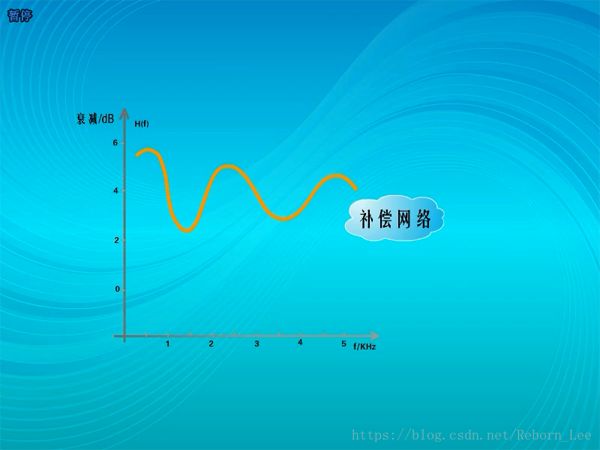
通過產生波形去補償失真波形，這種均衡則稱為時域均衡

對于dB的介紹：

dB也稱為分見，是一個計量信號增益或衰減的相對值的單位。以電話發明家貝爾的名字命名，- -貝爾等于10分貝。分貝在1924年首先被應用到電話工程中,1968年被CCITT (國際電報電話咨詢委員會)采納，作為通信系統的傳輸單

dB表示的是兩個量的比值的大小，直觀可理解為倍數越大，dE也越大。對于電壓、電流等振幅類物理量，通常將測量值與基準值相比后求常用對數再乘以20 dB= 201g[A7/B)) ;對于電壓、電流等的平方項，如能量或功率等，則取對數后再乘以10 ( dB=10lg(A/B) 1

使用dB的好處：
?

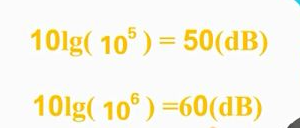
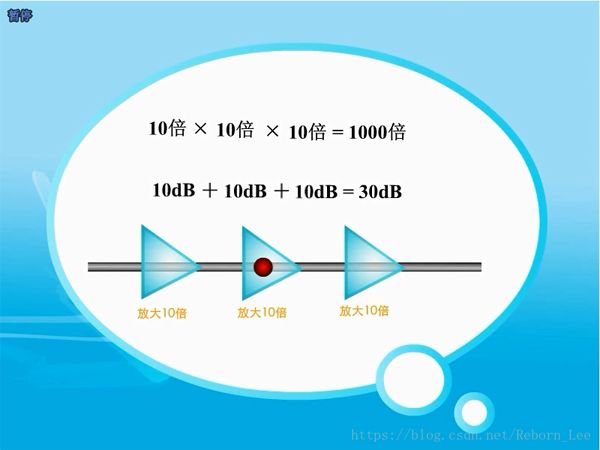
第二大好處:符合聽感

無線信道：

電磁波的傳播方式：直射、散射、反射、繞射；

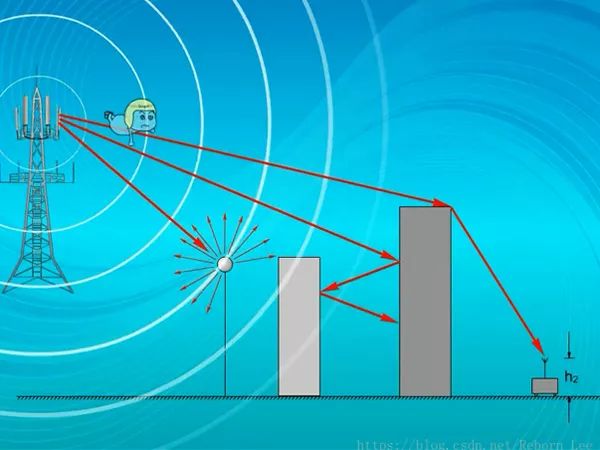
無線信號的衰減方式：

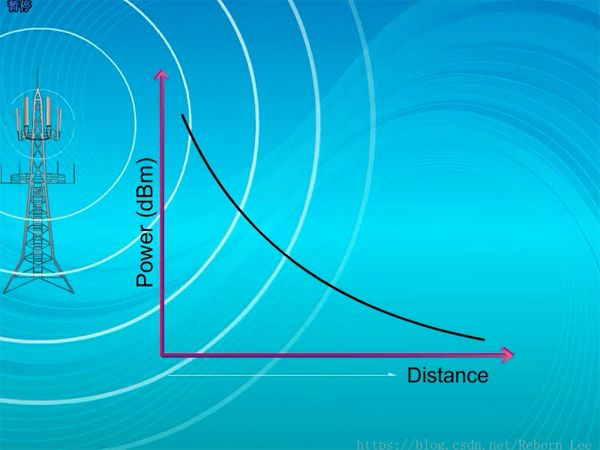
自然衰減（路徑損耗）：（大尺度衰落）

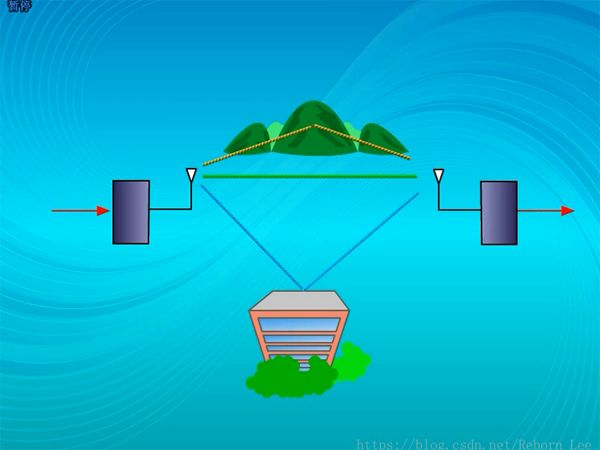
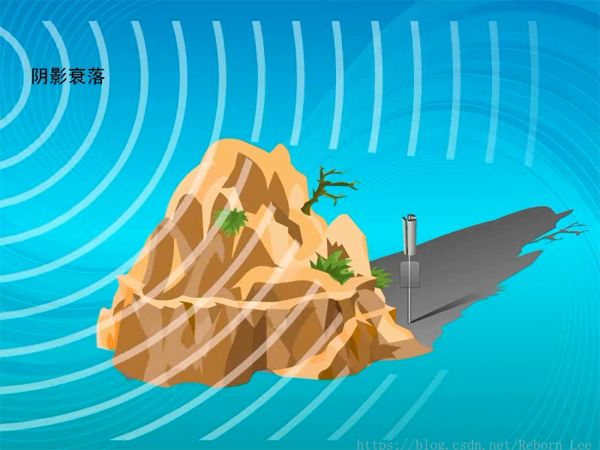
第二種衰減是遇到起伏的地形，建筑物等，因為阻塞而造成的衰減；（中尺度衰落）

這種衰減又叫陰影衰落，就像陽光產生的陰影一樣

第三種衰落由電磁波的多徑傳輸引起，又叫瑞利衰落；（小尺度衰減）

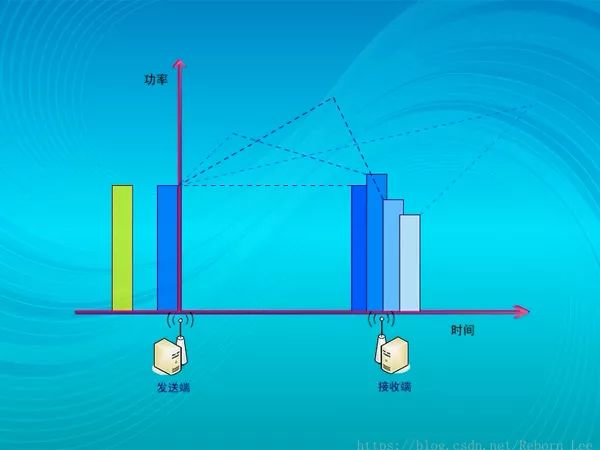
無線信號從天線發出后，要經過不同路徑到達接受端；

例如經過直射，反射、繞射等到達接收機，由于各路徑距離不同，長短不一；

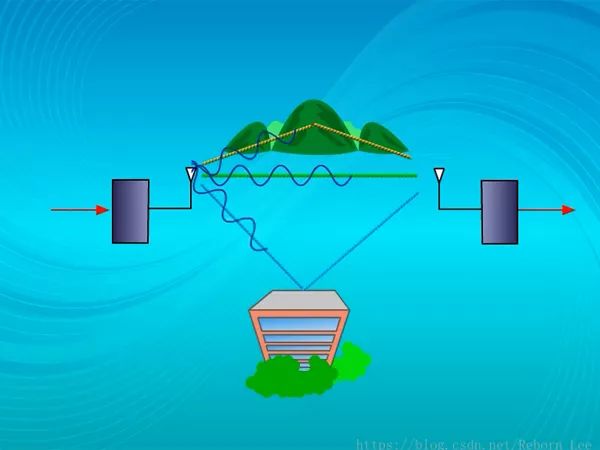
因而各條發射波到達接收機的時間，或者說相位各不相同，這相當于不同相位的信道在接收點疊加；

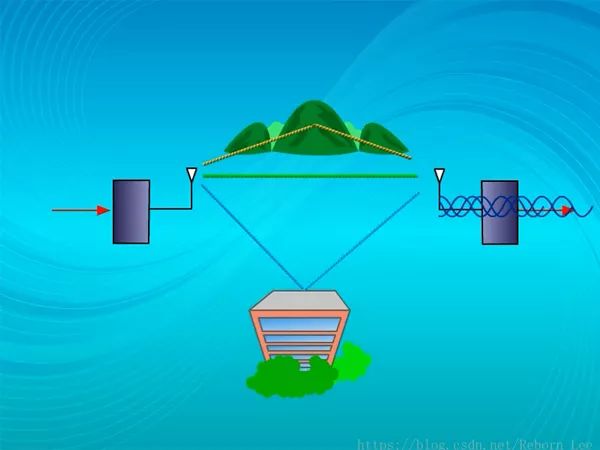
如果同相信號疊加，信號的幅度會加強，而反向疊加，信號的幅度則會被減弱；

這樣信號的強度會發生急劇的變化；

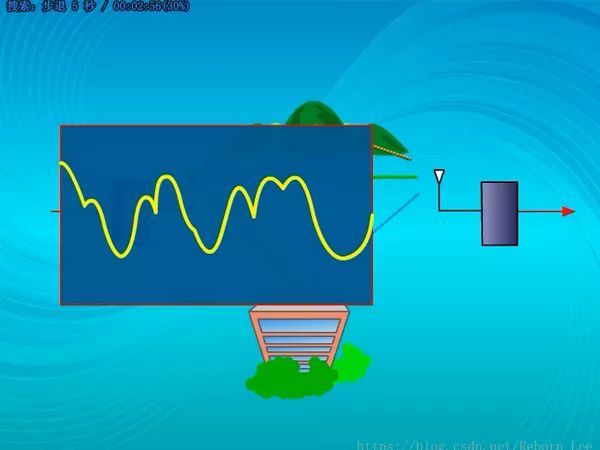
就像這樣，信號的幅度在很短的距離內，就發生深度衰落，衰落程度達到20~50dB，這就是說每隔幾米，就會有100倍到10完倍的落差；其間還有數千個淺衰落，這就是瑞利衰落。（小尺度衰減，因為發生衰減的范圍很小）

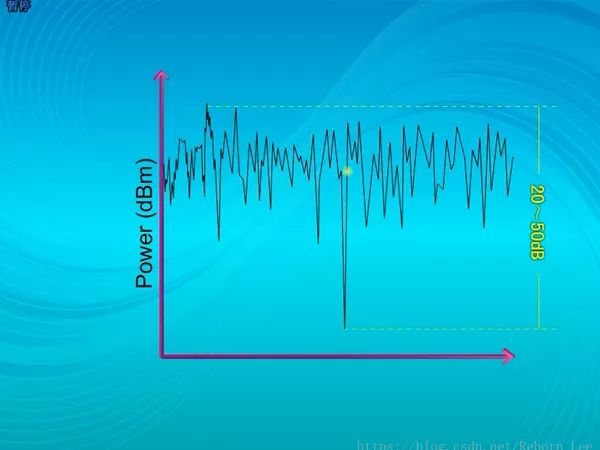
瑞利衰落是無線信道的最大問題，其他兩個衰落解決辦法相對容易；

例如路徑損耗，當信道衰落到一定程度后，可以通過加中繼放大器來加強信號；正是由于這種衰落，我們才可以每隔一定的距離，當某段頻率的信號衰減為0后，再設一個基站，重復使用這一段頻率 ，這樣能極大的提高頻譜的利用率，這也是移動通信網絡普遍使用蜂窩組網的原因。

陰影衰落：

當衰落比較嚴重時，可以在陰影的地方加一個信號放大器，也叫直放站（室外）；

科普：

直放站是一種無線信號中繼產品，衡量直放站好壞的指標主要有，智能化程度（如遠程監控等）、低IP3（無委規定小于-36dBm）、低噪聲系數（NF）、整機可靠性、良好的技術服務等。

使用直放站作為實現“小容量、大覆蓋”目標的必要手段之一，主要是由于使用直放站一是在不增加基站數量的前提下保證網絡覆蓋，二是其造價遠遠低于有同樣效果的微蜂窩系統。直放站是解決通信網絡延伸覆蓋能力的一種優選方案。它與基站相比有結構簡單、投資較少和安裝方便等優點，可廣泛用于難于覆蓋的盲區和弱區，如商場、賓館、機場、碼頭、車站、體育館、娛樂廳、地鐵、隧道、高速公路、海島等各種場所，提高通信質量，解決掉話等問題。

室內稱之為：室內分布系統

綜上，解決路徑衰落以及陰影衰落的思想是加中繼放大器，但此方法對瑞利衰落并不適用。

解決瑞利衰落的方法是：

相干帶寬與相干時間：

無線信道較之于有線信道，復雜的原因在于多徑與時變，不過有兩種情況可以使無線信道變得簡單，那就是相干帶寬和相干時間；

由于多徑傳輸的原因，假如在發送端發送一個窄的脈沖信號，在接收端會接收多個脈沖，本來最短時延是沿最短路徑傳輸所消耗的時間，現在因為多條路徑長短不一，所以時延被擴展了，通常將最后一個到達的脈沖，和最先到達的脈沖的時延差，稱為最大時延擴展，用??來表示最大時延擴展。

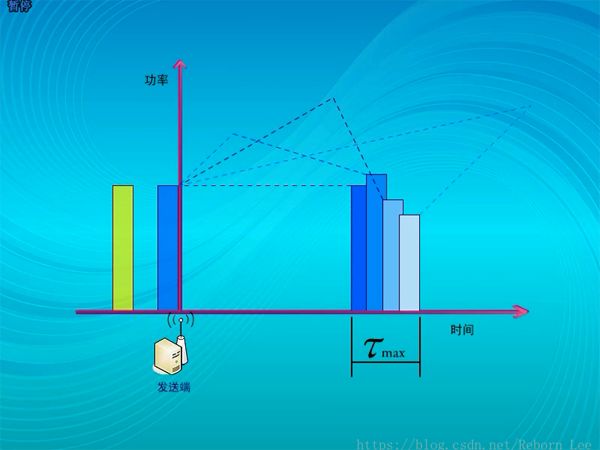
如果這個時延擴展大于兩個發送脈沖之間的時間間隔，則會對下一個脈沖的接收產生干擾；

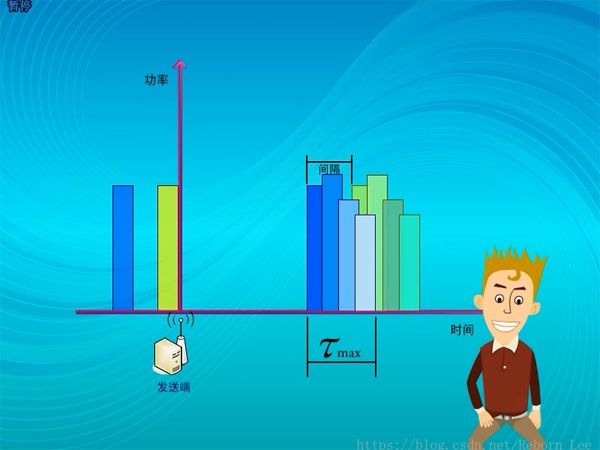
如果將這兩個脈沖看成符號，這稱之為符號間干擾；

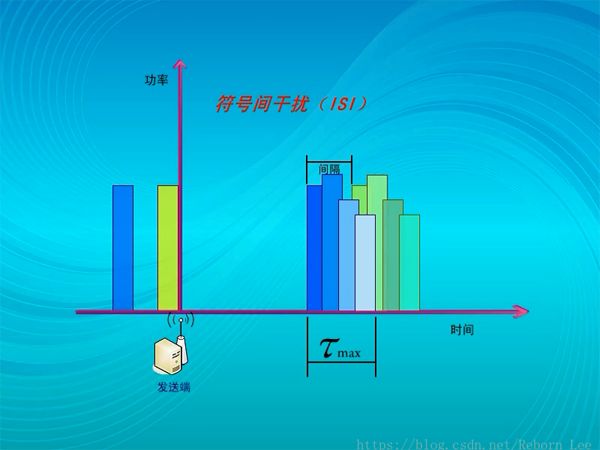
也就是接收信號中一個符號的波形因擴展到其他符號中而造成的干擾，要避免這種干擾，就要將發送符號之間的周期擴大，也就是把符號的寬度擴大，擴大多少呢？至少是大于最大時延擴展? Tmax；

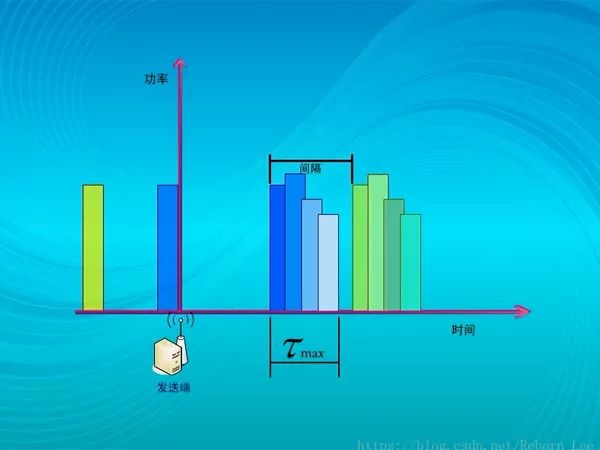
而周期擴大了，就意味著速率降低了，速率降低，也就意味著帶寬降低了；

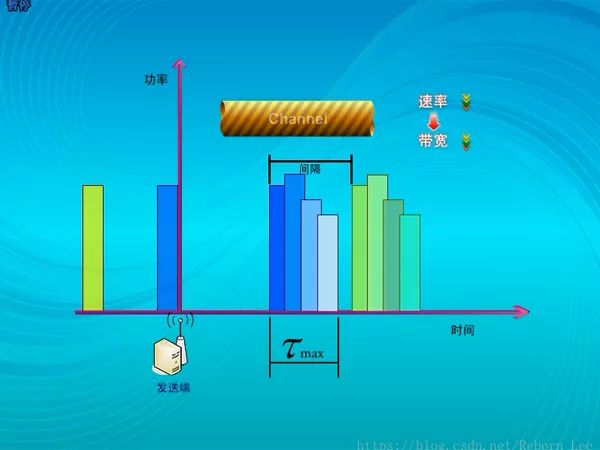
頻率選擇性衰落：

綜上，發送的符號的寬度必須大于最大時延擴展Tmax，這樣才能避免符號間的干擾，這相當于存在一個最小的周期Tmin，由于周期的倒數是頻率f=1/Tmin，所以就應該存在一個最大的頻帶寬度fmax=1/Tmin?，當信號的帶寬大于這個頻帶寬度時，就會發生干擾，這個帶寬就稱為相干帶寬；通常是用最大時延擴展的倒數來定義相干帶寬的：(ΔB)c=1/Tmax?；信號的帶寬大于相干帶寬時，就會發生頻率選擇性衰落。

符號間干擾和頻率選擇性衰落，實質是一樣的，在時域中是符號間干擾，表現形式是信號波形會發生畸變，換算到頻域中來看，就是有些頻率分量的強度會加強，有些會減弱，這種現象就稱為頻率選擇性衰落。這里只是部分頻率分量的信號會衰落，不是所有的頻率分量的信號都衰落，所有頻率分量的信號都衰落，叫做頻衰落。

那么高速通信怎么辦呢？高速信號的帶寬要大于相干帶寬吧？

對于帶寬大于相干帶寬的信號，如下處理：

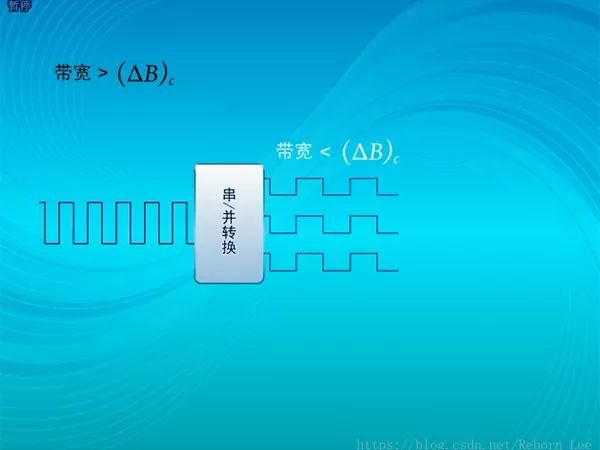
通過一個串并轉換器，將高速信號變為低速信號，這樣每路信號的帶寬就會小于相干帶寬。

在分別由不同的載波發送：

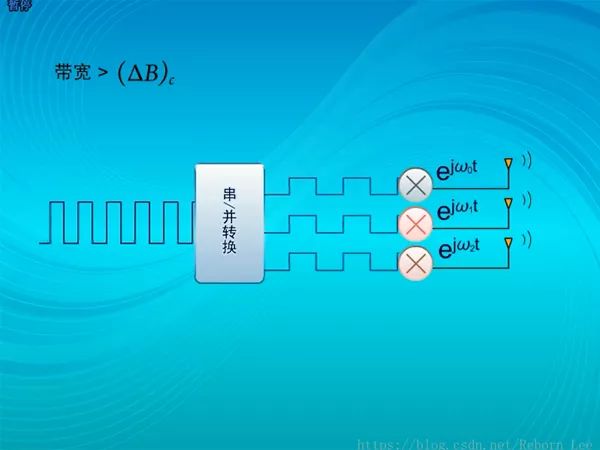
目前，較為熱門的正交頻分復用就是采用這樣的方法。

信道里的噪聲：

人為噪聲主要來自電臺、家電等電氣設備所產生的干擾。自然噪聲來源于自然界存在的雷電、磁暴、太陽黑子和宇宙噪聲等。宇宙噪聲主要是指天體輻射波對接收機形成的噪聲。

內部噪聲來源于系統設備本身產生的各種噪聲，如熱噪聲和散彈噪聲等。熱噪聲是由電阻性元器件中自由電子的不規則運動引起的;而散彈噪聲則是由電子管和半導體器件中電子發射不均勻而產生的。

熱噪聲、散彈噪聲和宇宙噪聲，由于其波形變化不規則，所以又被統-稱為起伏噪聲。

起伏噪聲是影響通信系統的主要噪聲，其他的噪聲我們可以忽略，起伏噪聲是一種隨機的信號；

隨機信號？

隨機信號是指這么一種信號，雖然它的波形也是時間的函數，但其在任意時刻上的取值是不確定的；

確知信號在某一時刻的取值是確定的，而隨機信號在某一時刻的取值是不確定的，但取值往往有一定的規律，規律往往可以用一概率密度來表示；

隨機信號更普遍一點叫隨機過程，是功率信號來的，它的頻譜沒有實際意義，因此不能直接用傅里葉變換直接分析它的頻譜，但可以用功率譜來分析，隨機過程的功率譜分析和確知信號的功率譜分析是一樣的，也就是它的功率譜密度和自相關函數是和確知信號一樣的，也是一對傅里葉變換的關系，對于一些難以得到功率譜密度的地方，可以通過求自相關函數來得到。

下面這種均勻分布的噪聲稱之為白噪聲；

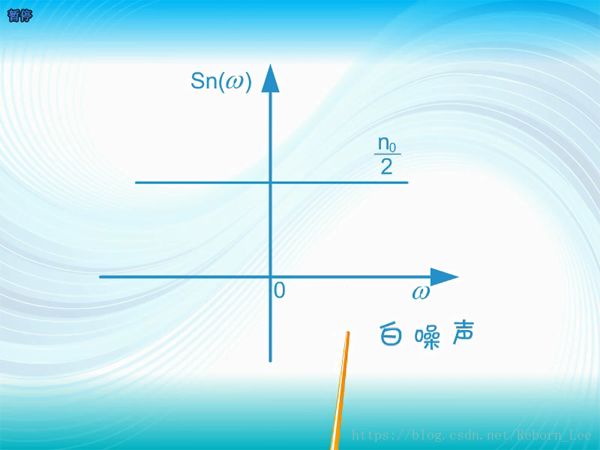
由于起伏噪聲的功率譜在相當寬的頻率范圍內也是均勻分布的，且概率密度服從高斯分布，因此也將起伏噪聲定義為高斯白噪聲；

此高斯白噪聲的自相關函數如下：

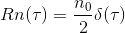
T是時間差，由此可見，高斯白噪聲任意兩個不同時刻之間毫不相關，這是一種十分理想的自相關特性；

研究CDMA系統的人十分羨慕高斯白噪聲，下面解釋原因：

介紹CDMA：

CDMA是碼分多址，是手機使用的一種無線技術；

CDMA的關鍵是擴頻通信，而擴頻通信的初衷是解決戰場上的保密通信問題，為了實現保密通信，需要將信號偽裝在噪聲之中，這首先就要擴頻，將窄帶信號功率分散在一個比較寬的頻譜范圍內，以降低單位頻帶上的功率，使信號淹沒在噪聲中，達到保密的目的，過程如下：

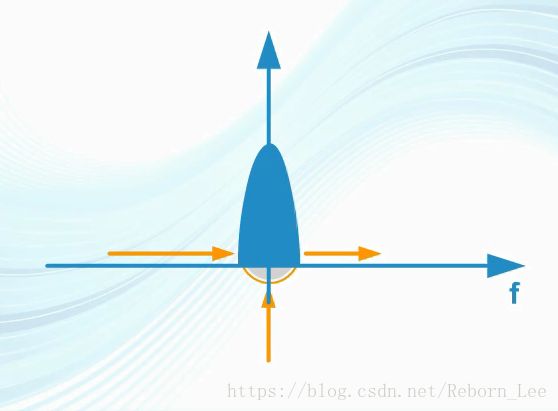
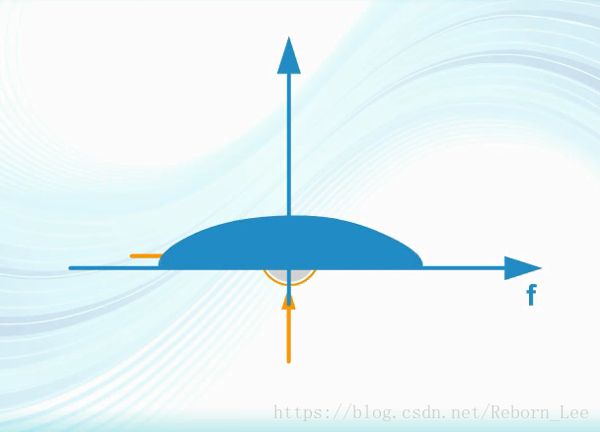
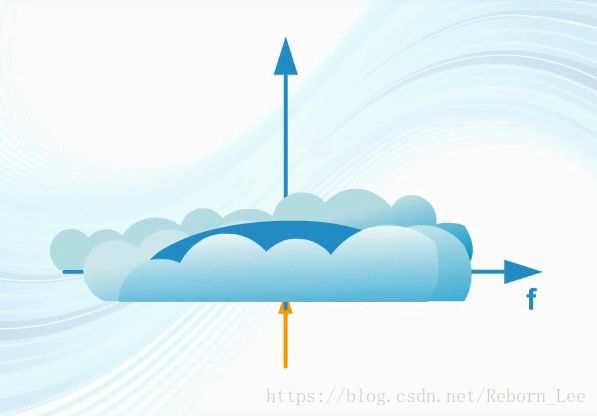
其次，信號要偽裝的像，擴頻后的信號要有接近白噪聲的特點，這主要是功率譜密度和自相關函數要像；

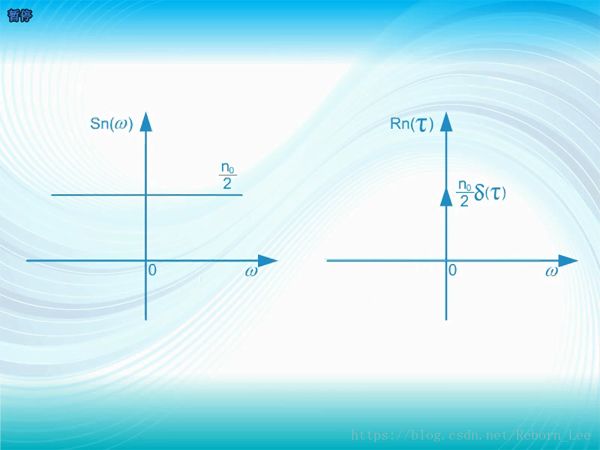
于是這幫人開始尋找一種優良的碼序列，以便使擴展出來的信號接近白噪聲的特點；

我們又知道，低速率的信號，帶寬窄一些；

高速率的信號，帶寬寬一些；

帶寬大概是速率的1/2；

低速率信號與高速率信號相乘，相當于它們的頻譜在頻域中卷積，卷積的結果是頻譜被展寬了，寬度是兩路信號的帶寬之和；

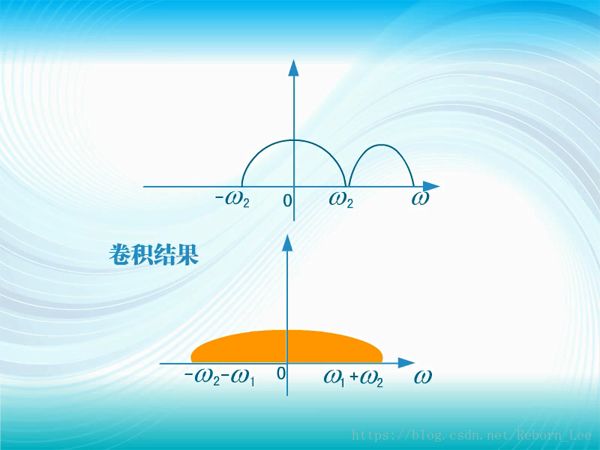
這就是說，他們要找的擴頻碼，首先要有一定的碼速率，要比被擴展信號的碼速率高好多倍，通常認為至少要高100倍；

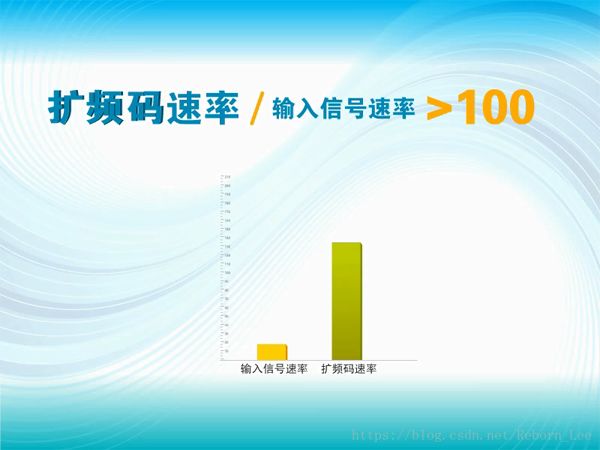
其次這個碼要是一個隨機碼，否則，怎么能說像白噪聲呢？

再次，這個碼的自相關函數和白噪聲的自相關函數也要像；

經過一番艱辛的尋找，終于找到了幾種，其中一種稱之為m序列，既有隨機的特點，又好制造，于是后來的許多擴頻系統都使用了這種m序列的隨機碼來擴頻，當然這種碼也不是完全的隨機碼，它只在一個周期內是隨機的；

到了下一個周期又從頭再來了；

所以，都將這種碼叫做偽隨機碼；

雖然是偽隨機的，但在一個隨機周期內，它的隨機表現還是相當不錯的，很接近白噪聲；

這從它的自相關函數中可以看出；

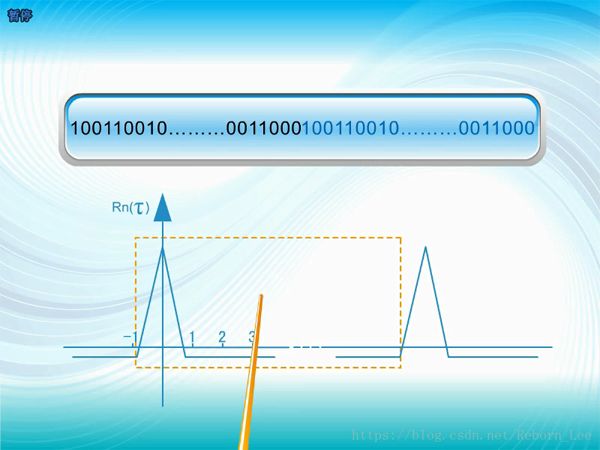
虛線框中是它的一個偽隨機周期，可見它的自相關函數很接近白噪聲的沖擊形狀了；

這么尖銳的自相關特性表明了現在的它和過去的它，跟將來的它，都是割裂的，不相關的；

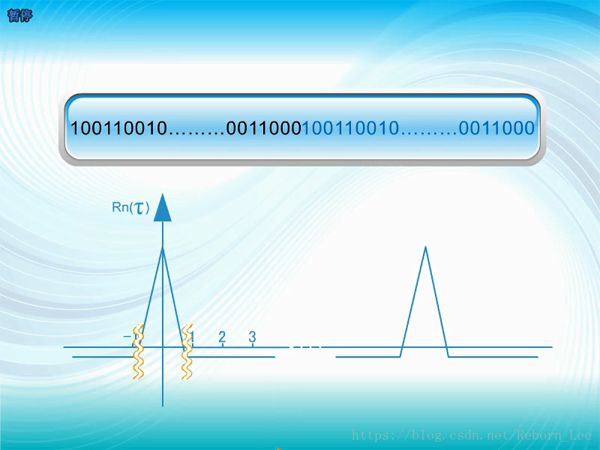
這個研究CDMA那幫人解決地址碼提供了另一種選擇；

什么是地址碼？

所謂的地址碼，就是用來區分不同用戶，或者基站的號碼；

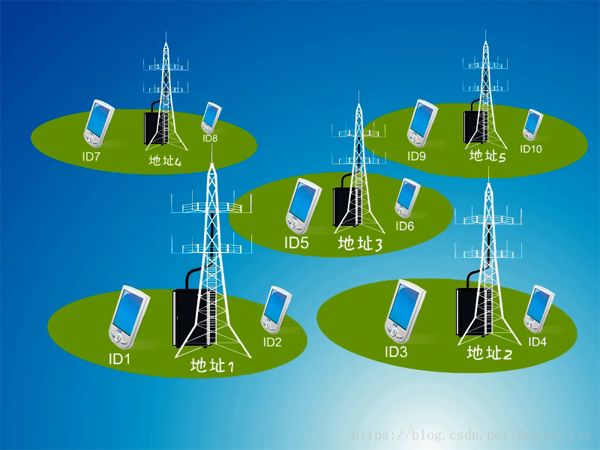
本來不同的m序列因為互相關特性大于0，不正交，因而是不適合作地址碼的，但同一個m序列，由于自相關特性十分尖銳，因此只要將產生m序列的碼發生器延遲不同的時間開始，那么所產生的隨機碼應各自不相關，也就可以當做地址碼來使用了，當然最大的延遲是不能超過它的隨機周期的；

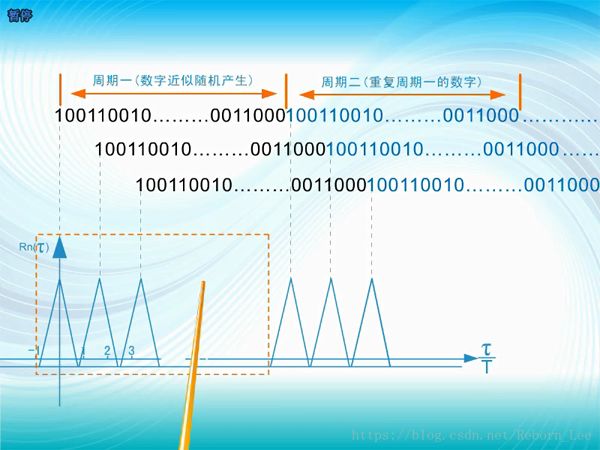
而為了確保各碼發生器，能在不同的延時上造碼，需要有一個統一的時鐘，來供各個碼發生器來參考。

對話信道容量：

面對一個存在高斯白噪聲干擾的信道，它每秒到底能無差錯傳輸多少信息量?這是每一個通信系統的設計者一直以來都渴望知道的，卻也一直都不容易解答的課題。

這便是香農公式；

C是信道容量，也就是信道所能傳輸的最大信息速率，單位為bit/s，B是信道的帶寬，S是信號的平均功率，N是白噪聲的平均功率，S/N稱為信噪比；

這個公式說明了什么樣的通信系統是理想的；

首先是當給定信號帶寬B和信噪比時，信道的極限傳輸能力，或者說信道容量也就確定了，如果信道實際傳輸的信息速率小于或等于信道容量，那么可以做到無差錯傳輸，或者說差錯率可以任意小；

但如果傳輸速率大于等于等于信道容量，那么信道就不可能無差錯的傳輸了；

其次增加信道帶寬B，或者提高信噪比，可以增加信道的容量，但如果不想要增加信道容量，而是保持信道容量恒定，哪款帶寬和信噪比之間是可以互換的，比如增加帶寬可以換取信噪比的下降，CDMA和擴頻通信的靈感，就是這么來的；

通過擴頻使信號功率與噪聲功率的比值得以降低，從而可以使信號淹沒在噪聲中；

問：要是不停的增加帶寬，是不是可以實現超高速通信了？

首先，頻帶十分寶貴；

其次就算頻帶可以無限制的增加，信道容量也不會跟著無限制的增大，這是因為這里面存在著高斯白噪聲，隨著帶寬的增加，噪聲的功率也會增大，那么信噪比同時也會降低，當信噪比低到一定程度時，再怎么增加帶寬也不能無差錯的傳輸信息了；

這就是說即使信道帶寬無線增大，信道容量也只能達到一個有限的數值了；

理論上推算出來的結論是，當信道帶寬很大時，或信噪比很小時，信道容量趨近于信號功率和噪聲功率譜密度之比的1.44倍；

由香農公式又是怎么得到4G的一個關鍵技術呢？

所謂4G,根據ITU (國際電信聯盟)的定義，至少應符合以下兩點:

1.移動狀態下數據速率達100Mbit/s;

2.室內靜止狀態下數據速率達1Gbit/s。

1.移動狀態下數據速率達100Mbit/s;

2.室內靜止狀態下數據速率達1Gbit/s。這比3G的標準速率至少提高了50倍。如何才能提高3G的信道容量，使之達到4G的標準呢?

要提高信道容量，香農公式指出了兩條明路：

（1） 增加信道帶寬；

（2） 提高信噪比；

由于頻帶資源有限，增加50倍的帶寬太奢侈，不現實，因此技術研究的落腳點是在提高頻譜的利用率上，這點OFDM能夠提供最佳的頻譜利用率，但光這，還遠遠不能達到4G的容量要求，因此還得雙管齊下，在提高信噪比上下一番功夫；

提高信噪比，是否可以加大信號的發射功率呢？

加大信號的發射功率對人體健康的影響是最大的問題，所以不能指望提高信號的發射功率來提高信道的容量，那要怎么樣才行呢？

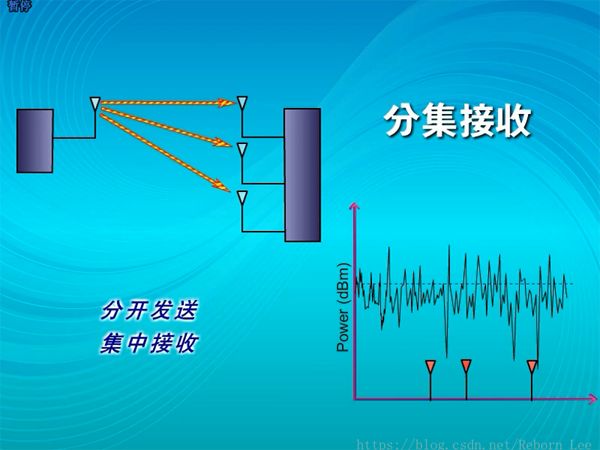
前面，在比喻多徑衰落的影響時，用到了空間分集，也就是使用多面天線也接收或發送信號；

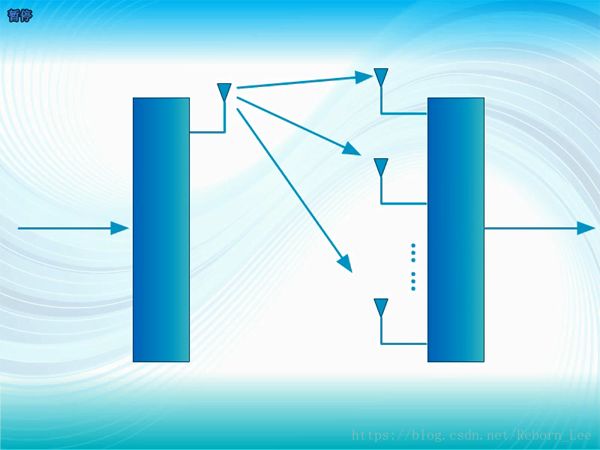
使用空間分集后，接收端合并接收多路信號，或者選擇其中最強的一路接收，其信號功率當然比只接收一路的強，而噪聲功率又基本是沒變的，所以信噪比自然就提高了；

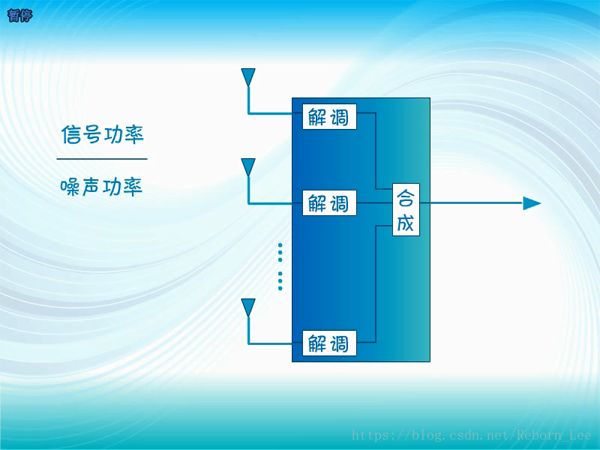
空間分集只在一邊使用了多面天線，或是在發射端，或者是在接收端，就已經提高了信道的信噪比，那么如果兩邊都同時使用多面天線，會提高多少呢？

這個問題難不倒通信大師，他們通過理論推算，得到了一個近似的容量公式；

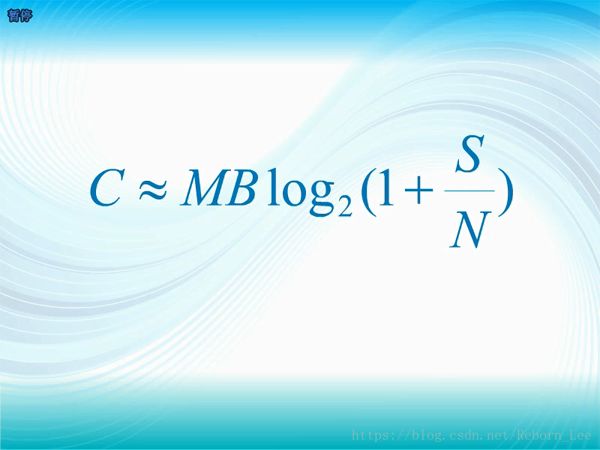
這個信噪比是每條接收天線上的信噪比；

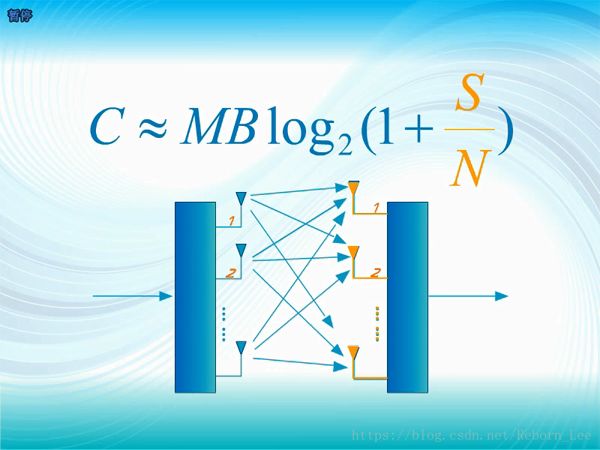
和香農公式對比發現多了一個M；

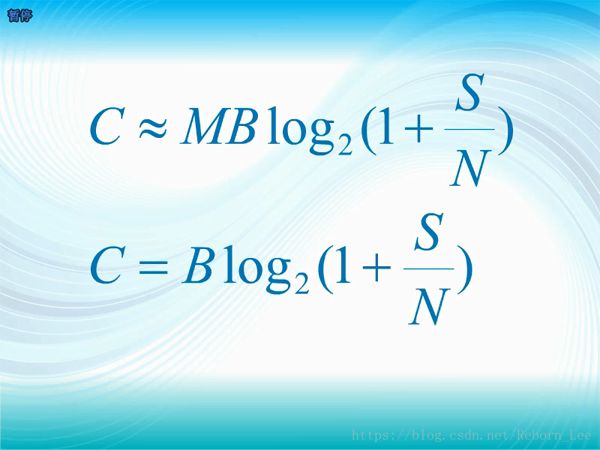
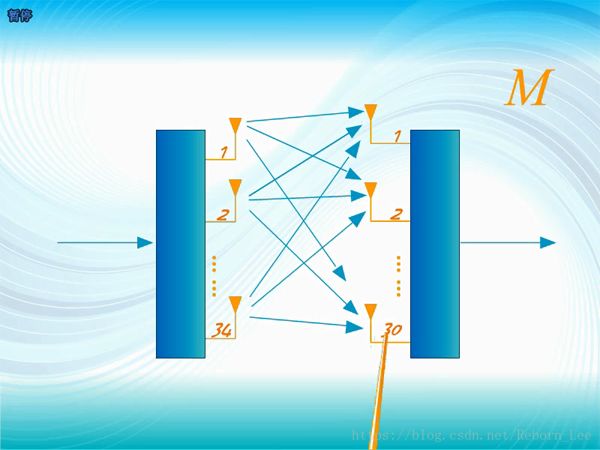
M是發送端或接收端的天線數；

哪一端的天線數少一點，M就代表那一端的天線數，比如發送端的天線數是2，接收端的天線數是3，則M= 2；

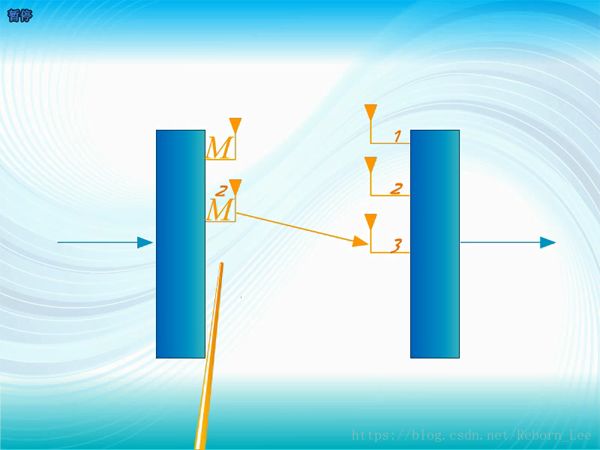
M的意義是什么？

M的意義是即使信噪比，和信道帶寬，都不增加，單獨增加天線對的數目，也可以直線增加信道容量；

這就是說信道的容量除了增加帶寬和信噪比以外，還可以通過增加天線的數量向空間索要，維特比，CDMA的創始人之一，他也說過，在多用戶接入系統中，空間處理仍然是最有前途的。

多面天線發送，多面天線接受的情形，稱為MIMO，MIMO是多輸入多輸出的簡稱，是當前無線接入研究的熱點。

什么是極化分集？

極化分集是在接收端分別接收水平極化波，和垂直極化波的一種分集方法；

極化是描述電磁波場強方向變化的一個概念，簡單的了解，就是水平極化波，和垂直極化波在信道中的衰落是獨立的，相關性很小，而即使發射天線只發射單一的極化波，在傳輸過程中也會演變成兩種極化的波，因此在接收端，就可以在垂直極化和水平極化上進行接收；

除了空間分集，極化分集，還有頻率分集，時間分集，角度分集等等，其實不同分集的原理是相同的，它們的前提都是要保證不同路信號之間，互相獨立，而接收時，則把不同路信號進行合并，選擇其中信噪比最大的一個作為接收信號，或者直接合并所有路的信號。

香農公式給出了極限的信息傳輸速率，我們都知道極限的東西當然是不容易超越的，只能不斷接近，那么在實際的通信系統中，都采用什么方法接近這種極限的呢？

歸納起來，就兩個辦法，編碼和調制。

作者：李銳博恩（Reborn）

編輯：黃飛

?