1 前言
并聯電容器是電力系統的重要無功電源,具有成本低、便于維護和運行、經濟效益好等特點。電容器在系統中會產生以下現象:①與電力系統的感性設備發生諧振;②因絕緣老化和發熱等,造成系統短路;③投入系統時產生無功沖擊,出現較大的涌流等。其中諧振和絕緣問題是電容器組設計、投運和運行中所要考慮的首要問題。本文結合電容器組的設計論證和對河南電網部分變電站的諧波測試,對電容器的過電壓和過電流問題進行討論。
2 并聯電容器組諧波過載能力的四條要求
2.1 反映電容器耐壓性能的指標:過電壓倍數
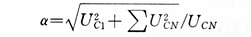
國標《并聯電容器裝置設計規范》(GB50227-1995)規定:α≤1.1,表示電容器所承受的基波電壓與諧波電壓的幾何和(電壓有效值)不超過額定電壓的1.1倍。作為算法上的對比,計算基波和諧波電壓的算術和時:
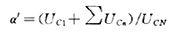
2.2 反映電容器耐熱性能的指標:過電流倍數
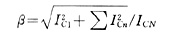
國標《并聯電容器裝置設計規范》(GB50227-1995)規定:β≤1.3,表示流過電容器的基波電流和諧波電流的幾何和(有效值)不應超過額定電流的1.3倍。作為算法上的對比,計算基波和諧波電流的算術和時:
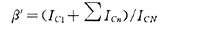
2.3 反映電暈現象的指標:峰值電壓過電壓倍數
IEEE規定:γ≤1.2。顯然γ=α′。
2.4 考慮過載容量的指標:過載容量倍數
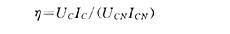
IEEE規定η≤1.3,即過載容量不超過額定容量的1.3倍。根據過壓倍數、過流倍數計算方法的不同,η值可以是αβ、αβ′、α′β和α′β′。
3 河南電網部分變電站實測結果和計算
3.1 駐馬店220kV變電站的電容器過電壓過電流的計算
首先,將10kV母線的電壓諧波數據(見表1)轉化為電容器端電壓的諧波。電容器串聯電抗器,電抗器基波電抗為XL,電容器基波容抗為XC,母線基波電壓為U1,諧波次數為n,n次諧波百分含量為DFVn,母線n次諧波電壓為DFVn·U1,n次諧波電抗為nXL,n次諧波容抗為XC/n。那么,電容器n次諧波電壓百分含量為:
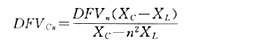
由表2知,采用算術和的計算方法表明電容器已過電壓,最大峰值過壓倍數接近1.2,符合峰值電壓校驗。實際運行情況是電容器接近過電壓的限值。因為母線電壓沒有達到母線保護的定值(平均電壓的1.1倍),電容器電壓的有效值也沒有達到額定電壓的1.1倍,所以母線過電壓保護和電容器分支過電壓保護不動作。
??? 表3,說明變壓器低壓側電流沒有超過《并聯電容器裝置設計規范》的定值。利用駐馬店站的設備實際參數,計算得到投入電容器后,諧振頻率在230Hz附近,大電流并非諧振造成,10kV母線運行電壓過高才是電容器的運行電流過大的原因。
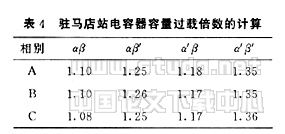
??? 表4說明在利用算術和算法求電壓電流時,才判斷電容器容量過載。事實上容量不過載。
3.2? 薛坡220kV變電站過電流過電壓的計算
??? 薛坡220kV變電站是許昌供電區的樞紐站,帶有電鐵負荷。1998年以前,該站電容器組不能正常投運,串聯電抗器嚴重發熱。1999年1月12日,測試了薛坡站的諧波。
??? 現場觀察和測試都表明,電容器的運行電流過大,β>β'更大,見表5。電容器不能安全運行,電流已超過保護整定值(額定電流的1.6倍),所以保護運作。
根據測試和計算,諧振頻率接近5次諧波而產生諧波電流的放大。這直接導致10kV側的5次諧波電壓和總畸變率超標,見表6。
表7是電容器端電壓的諧波值和過電壓倍數。α達到和接近1.1,α′>1.1,最大值為1.48,電流諧振造成過電壓,γ>1.2,峰值過電壓。
表8說明電容器容量過載,與實際相符合。(這是薛坡站1998年的情況。河南省電業局和許昌電業局于1999年對電容器組改造后,運行良好。)
3.3 通過以上實例,并聯電容器組諧波過載能力的四條要求中,前三條(耐壓、耐熱、峰值
電壓校核)是關鍵,如果耐壓、耐熱、峰值電壓校核合格,第四條容量校核也合格。由于峰值電壓校核實際上是計算電壓算術和,所以只要耐壓、耐熱校核合格,峰值電壓和容量的校核也合格。
4 結論
通過討論,結合駐馬店和薛坡兩站的實例分析,總結如下。
4.1 引起電容器過壓和過流的因素是復雜的,諧波諧振或運行電壓過高都可以使電容器過載,應具體問題具體分析。
4.2 電容器過載的四點規定是相互聯系的,其中(1)、(2)、(3)是最重要的,滿足前3條,往往滿足了(4)條。(3)條由于與電壓算術和的算法等效,所以實際工作中只要驗證(1)、(2)就可以了。
4.3 綜合考慮諧波電壓和電流的作用,可以有兩種算法:幾何和與算術和。與之對應的判斷方法:電壓(幾何和)—電流(幾何和)、電壓(幾何和)—電流(算術和)、電壓(算術和)—電流(幾何和)、電壓(算術和)—電流(算術和)。這四種方法得到的結論有較大不同。其中幾何和的算法,計算的結果是有效值,具有實際物理意義的,也是《并聯電容器裝置設計規范》要求的算法。所以在利用實測數據進行電容器過壓過流的判斷,宜利用電壓(幾何
和)—電流(幾何和)。
4.4 在進行電容器諧波論證時,從論證的裕度出發,采用電壓(算術和)—電流(算術和)
的方法,裕度最大。筆者贊成利用電壓(算術和)—電流(幾何和)及電壓(算術和)—電流
(算術和)的方法,其中后者的裕度最大,條件滿足后,峰值電壓和容量的校核也可滿足。
