零極點的理解是模擬電路最關鍵的基礎之一,信號與系統都會講自然響應,自然響應就是偏微分方程的通解部分,而受迫響應則是偏微分方程的特解。本文將詳解零極點與頻率響應之間的關系。
我們從頻率域來分析零極點的影響。從頻率域上,零點和極點會決定系統的頻率響應。我們令系統傳輸函數H(s)中s(=σ+jω) 的實部σ=0而虛部ω仍然是變量,就得到了頻率響應函數H(jω)。頻率響應函數代表系統在恒包絡正弦小信號輸入時,輸出正弦信號相對輸入正弦信號的幅度和相位變化。頻率響應函數可以表示為:
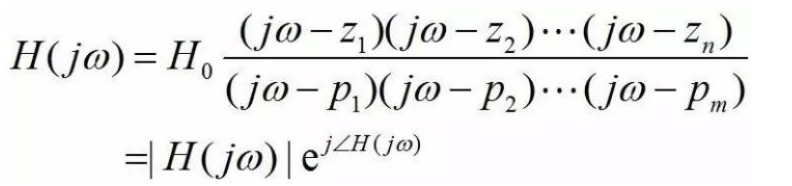
頻率響應H(jω)是復數。其幅度|H(jω)|代表當正弦信號頻率為ω時,輸出正弦信號幅度相對輸入正弦信號幅度的比值(即系統的增益),而其相位∠H(jω)則代表輸出正弦信號相對輸入正弦信號的相位變化。根據高中數學,頻率響應的幅度和相位可以表示為各個零點/極點的貢獻:
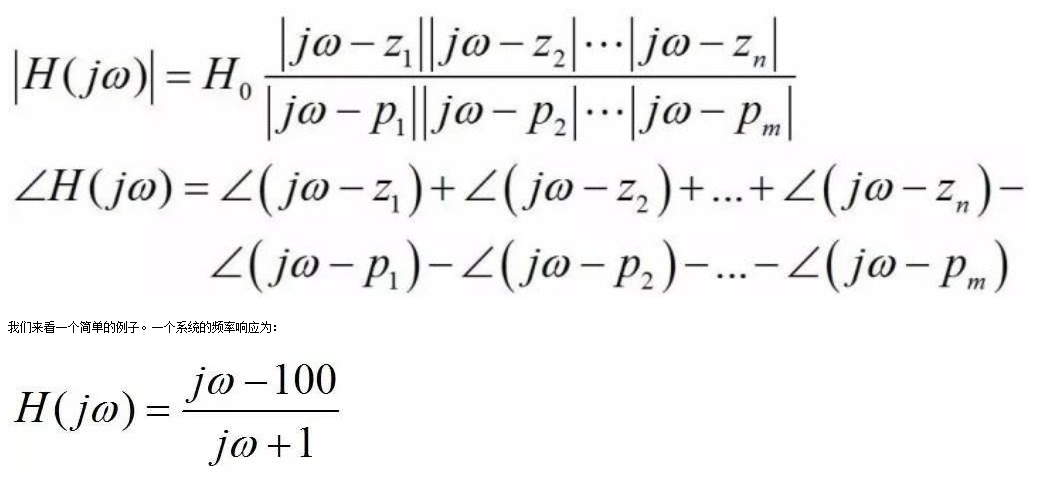
它有一個極點(實部σ=-1,虛部ω=0,其模為1)和一個零點(實部σ=100,虛部ω=0,其模為100)。由于極點的實部小于0,該系統是穩定的。當ω=0的時候[即DC(直流)響應],分母的模為1,相位為0,分子的模為100,相位為π,因此頻率響應的幅度為100,相位為π。我們接下來增加一點點ω,讓它等于0.001。這個時候ω遠遠小于極點的模,因此頻率響應分母的值和DC時沒有顯著區別(1+j0.001≈1)。ω也遠遠小于零點的模,因此頻率響應分子的值也和DC時基本相同。所以當ω的值遠遠小于某個極點/零點的模的時候,該極點/零點的效應可以忽略不計。這也是在實際電路設計中很多頻率遠高于電路工作頻率的極點/零點在分析的時候可以忽略的原因。當ω增加至1時,分母變為(j1+1),此時分母的幅度由DC時的1變為√2,相位則由0變為π/4。由于ω仍然遠小于零點(1《《100),分子較DC相比仍然沒有變化。頻率ω=1時對極點是一個轉折點:隨著ω繼續增長,該極點的效應漸漸變得顯著。當ω=10的時候,ω已經遠遠大于極點的模,因此頻率響應的分母可以近似為jω,相位為π/2。此后隨著ω繼續增長,分母的模隨之變大,因此在零點發揮作用前,頻率響應的幅度會隨著頻率增大以20dB/dec的速度減小。另一方面,當ω增大到遠大于零點的模(》》100)時,頻率響應的分子可以近似為jω,因此分子的相位為π/2,且分子的模隨著頻率增長以20dB/dec的速度增長。此時分子和分母的模都以20dB/dec增長,因此互相抵消,頻率響應的幅度不再變化,而相位則由DC時的π變為0。
H(jω)的幅度和相位
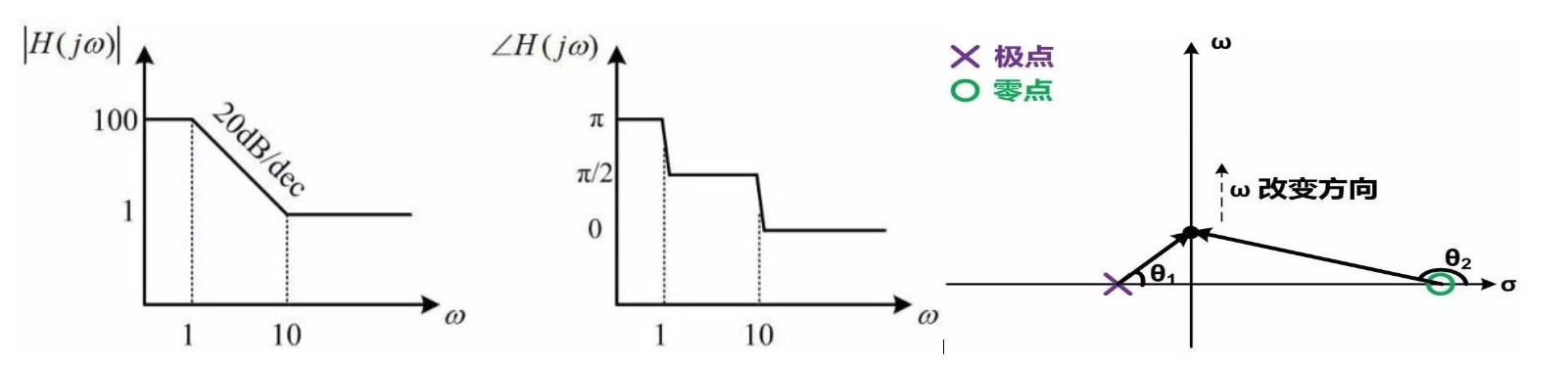
零點和極點對頻率響應的效果也可以由s平面零極點圖解釋。上面例子的零極點圖如下:
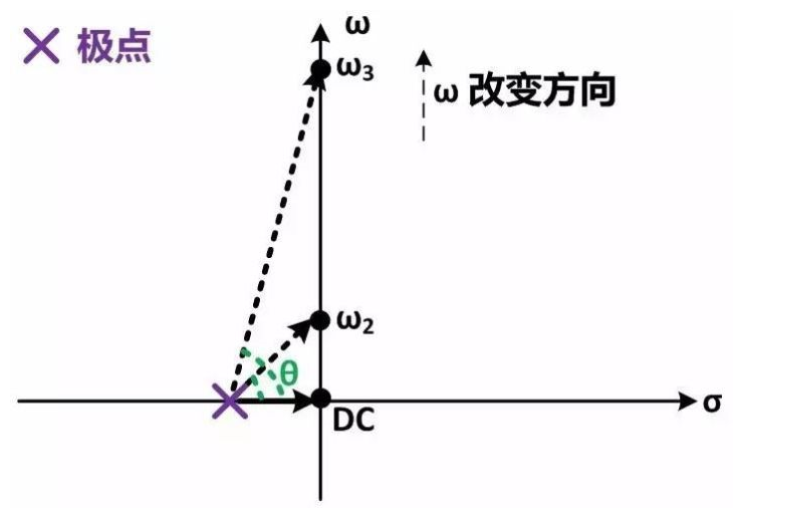
開始ω1=0 (即DC響應),極點向量的相位為0。之后隨著ω增加,極點向量的長度逐漸增長,相位貢獻θ也逐漸變大。當ω等于極點的模的時候(ω2),根據初中數學極點向量的長度變為DC時的√2倍,而相位角θ為π/4。之后隨著ω繼續增長到遠大于極點的模的時候,極點向量漸漸變得和ω軸平行,此時極點向量的長度近似等于ω,而相位角θ也漸漸逼近π/2。對于零點也可以做類似的分析。這樣圖解分析與之前分析的結果相同,但是更直觀。
