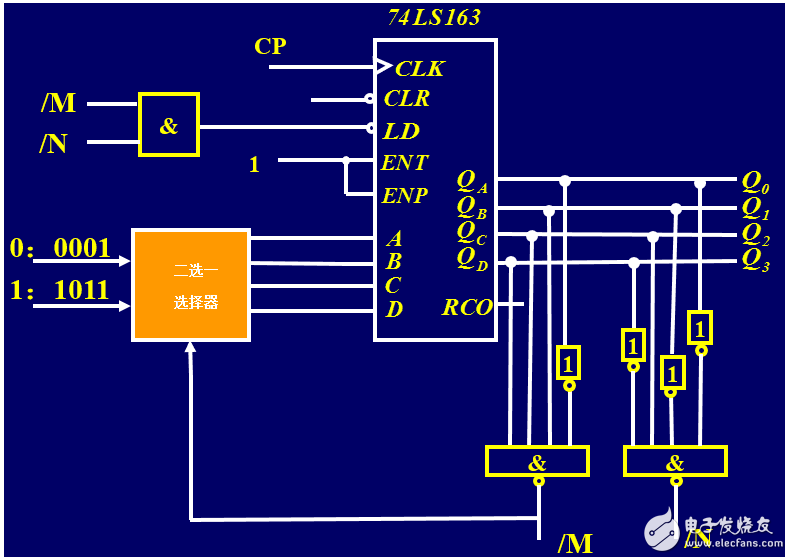
74LS163是常用的四位二進制可預置的同步加法計數器，他可以靈活的運用在各種數字電路，以及單片機系統種實現分頻器等很多重要的功能。

74ls163引腳圖

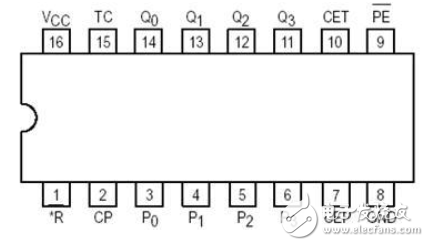
74ls163引腳功能

時鐘CP和四個數據輸入端P0~P3清零/MR使能CEP，CET置數PE

數據輸出端Q0~Q3

以及進位輸出TC.（TC=Q0·Q1·Q2·Q3·CET）

74ls163功能表

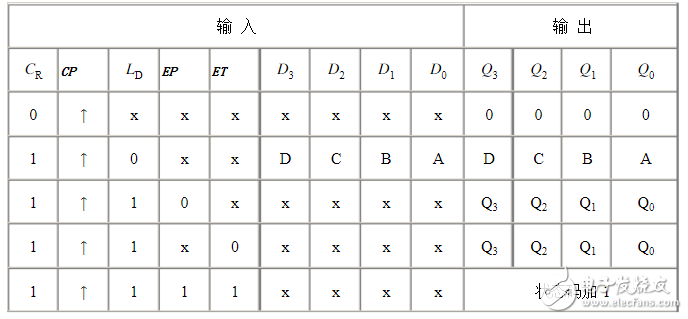
從74LS163功能表功能表中可以知道，當清零端CR=“0”，計數器輸出Q3、Q2、Q1、Q0立即為全“0”，這個時候為異步復位功能。當CR=“1”且LD=“0”時，在CP信號上升沿作用后，74LS163輸出端Q3、Q2、Q1、Q0的狀態分別與并行數據輸入端D3，D2，D1，D0的狀態一樣，為同步置數功能。而只有當CR=LD=EP=ET=“1”、CP脈沖上升沿作用后，計數器加1。74LS163還有一個進位輸出端CO，其邏輯關系是CO=Q0·Q1·Q2·Q3·CET。合理應用計數器的清零功能和置數功能，一片74LS163可以組成16進制以下的任意進制分頻器。

74ls163應用電路

（一）以74LS163為基礎設計一個6分頻電路

首先，需要明白什么叫分頻，圖3展示了分頻的效果：

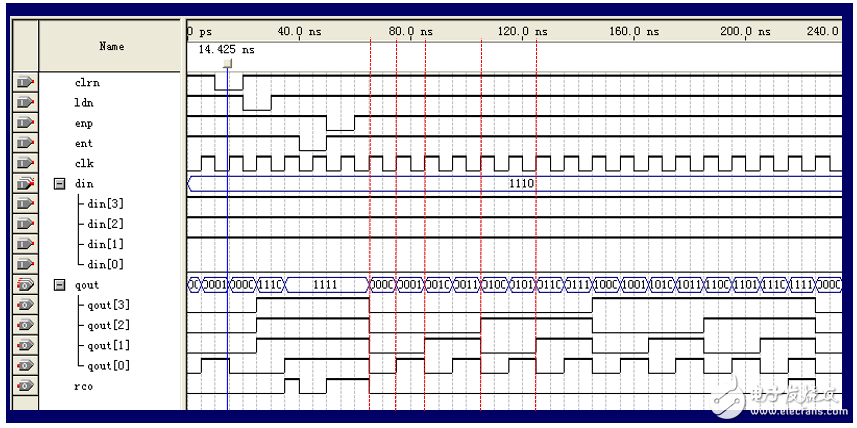
分頻通常以CP（時鐘脈沖）為基礎，從圖3中可以看出：qout［0］的周期為CP的2倍，qout［1］的周期為CP的4倍，qout［2］位8倍，qout［3］為16倍，顯然，其頻率分別為CP的1/2， 1/4， 1/8， 1/16，即所謂的2-分頻，4-分頻，8-分頻，16-分頻。

再進一步分析，對于qout［0］，其變化為：當一個時鐘脈沖來臨時，qout［0］變化一次；對于qout［1］，每兩個時鐘脈沖，qout［1］值變化一次；對于qout［2］，每四個時鐘脈沖，qout［2］值變化一次；對于qout［3］，每8個時鐘脈沖，qout［3］值變化一次。依次類推，如果要做6分頻，顯然應該是每3個時鐘脈沖，值變化一次，如何用74LS163來做6-分頻呢？

顯然，這個問題變為：如何使74LS163中的某一位每3個時鐘脈沖跳變一次。顯然，只有QD和QC這兩位的變化可能滿足（QB每兩個脈沖跳變一次，QA每個脈沖跳變一次），如果選擇QC，顯然可以找出一個序列：

0000 —》 0001 —》 0010 —》 1101 —》 1110 —》1111 —》0000 —》 …

對于QC，先是3個0，然后是3個1，開始循環，正好是6分頻。仔細觀察，發現這個循環對于QD也是6分頻。

針對上面分析得到的狀態遷移序列，如何用74LS163來實現呢？對于前半部0000 —》 0001 —》 0010，執行的是正常的計數功能，對于后半部1101 —》 1110 —》1111（ —》0000），執行的也是正常的計數功能，只有0010 —》 1101是一個跳躍，即當計數器狀態為0010時，下一個狀態需要用到163計數器的并行置數功能，因此，需要對163的計數器的輸出進行判斷，當輸出為0010時，用1101對電路進行置數（確保下一時刻電路狀態為1101）。

在此分析的基礎上，其電路圖如圖4所示：

（二）2421碼的模8電路

假設要求模8的狀態序列如下圖5所示：

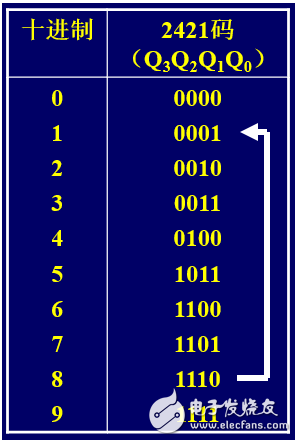
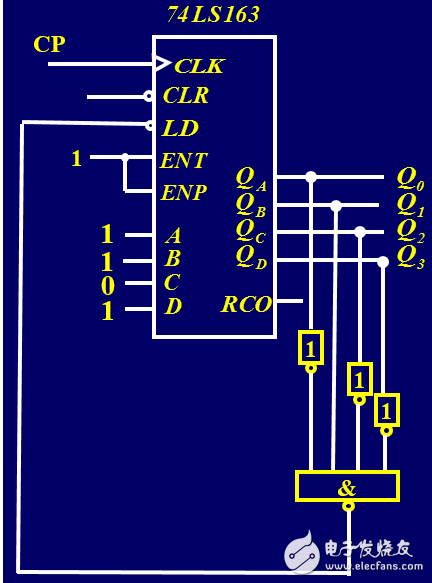
在圖5中，模8的狀態遷移序列為：

0001 —》 0010 —》 0011 —》 0100 —》 1011 —》 1100 —》 1101 —》 1110 —》 0001 —》 …

即：初始狀態為0001，當狀態為1110時，一輪計滿并遷移到狀態0001。

這個狀態遷移序列中，需要注意的地方包括：

- 初始狀態為0001，即初始時需要置位

- 序列前半部分 0001 —》 0010 —》 0011 —》 0100和序列后半部分1011 —》 1100 —》 1101 —》 1110執行的是正常的計數功能

- 0100 —》 1011有狀態跳躍，在到達狀態0100時，需要置數；1110 —》 0001，即記錄一輪滿時，需要置數

從上面的分析中得知，這個電路中存在兩次置數，一次為初始狀態的置數，另一個則為0100 —》 1011狀態遷移時的置數，并且兩次需要置的數值是不一樣的，其它情況正常計數。因此，置數的時候需要作二選一，即從兩個數中選擇一個置數，需要一個二選一的選擇器；另外，還要確定置數的時機，顯然，當狀態為1110時，需要置數為0001，當狀態為0100時，需要置數為1011。

由上分析可知，其對應的電路圖如圖6所示：