?
圖像傳感器的非均勻性直接影響了成像系統的探測靈敏度和空間分辨率,用這樣的成像裝置觀察景物,成像質量必然受到影響,甚至圖像會模糊不清. 因此,必須對非均勻性進行校正. 盡管針對非均勻性校正的研究多種多樣,但目前在商業上有推廣價值的還是2點法,專家和工程師們的著眼點依然是修正和完善2點法,如提高精度和算法處理速度. 此外,一些非線性校正方法,如神經網絡校正法、時域高通濾波器法還處于實驗室研究階段.
圖像傳感器光敏元的光電轉換特性曲線反映了其輸出(U )與輻照度(H)之間的關系,因此,非均勻性體現為各個光敏元具有各不相同的光電轉換曲線. 非均勻性校正的最終目的就是通過校正處理使得圖像傳感器所有光敏元表現出完全相同的光電轉換關系. 2點法是在光敏元的輸出與輻照度成線性關系的前提下建立的,它以某一直線作為標準,通過選擇合適的斜率和偏置校正系數,將所有光敏元的轉換特性均校正為與標準直線重合(即有相同的線性函數) ,從而使所有的光敏元在相同的輻照度下,有相同的輸出.
實際上,光敏元的輸出與輻照度兩者之間通常被認為服從拋物線模型. 顯然, 2點法所采用的線性近似是比較粗糙的,使其應用范圍局限于圖像傳感器光電轉換線性較好或工作范圍較窄的情況. 為此,筆者引入了多點校正方法,該方法將整個飽和輻照度區域劃分成若干子區域,每個子區域的光敏元輸出與輻照度的關系采用線性函數表示,從而能夠更好地逼近拋物線模型,并將圖像傳感器的工作范圍擴展到整個飽和輻照度區域. 為實現多點校正法,筆者設計了基于復雜可編程邏輯器件的硬件校正實現方案,實驗表明,該校正系統可將圖像傳感器CL512J的非均勻度由40%校正到2%. 因此,多點校正法及其實現系統能在不提高制造工藝和進一步研究光敏元結構的基礎上,有效地降低圖像傳感器的非均勻性,獲得較為理想的圖像質量.
1 非均勻性多點校正法
如果直接利用光電轉換關系的拋物線模型進行校正,硬件實現較為困難. 因此,引入多點校正法,利用分段線性函數來逼近非線性響應關系,即將整個飽和輻照度區域劃分成若干個子區域,每個子區域的光電轉換關系采用線性函數逼近,然后分別對每個子區域采用2點法進行校正處理. 顯然,多點校正法是2點校正法的擴展. 假設進行n點校正, 圖1給出了在輻照度子區域(Hj, Hj+1 ) ( j = 1, ., n - 1; Hj+1>Hj )的校正示意圖.
?
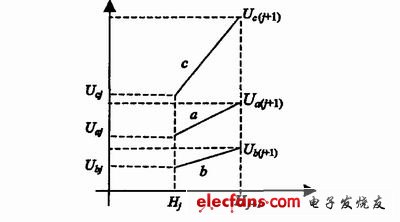
圖1 2點校正法示意圖
圖中,直線a和b分別表示圖像傳感器中a和b 2個光敏元在(Hj , Hj+1 )區域內的光電轉換特性的逼近直線,直線c表示校正后2個光敏元的轉換特性.
從圖1可看出,在Hj和Hj+1輻照度下,校正前a和b光敏元的視頻輸出值分別為Uaj、Ua(j+1) 、Ubj和Ub(j+1) . 由于非均勻性的存在,使得Uaj ≠Ubj、U a (j+1) ≠U b(j+1) . 校正后, a和b 2個光敏元在H j和H j+1輻照度下,均分別有相同的輸出: Ucj和Uc(j+1) . 同時也保證了在(Hj , Hj+1 )區域內,相同輻照度下2個光敏元均有相同的輸出. 直線i ( i = a, b)可表示為:
?
式中, Uij為i光敏元校正前的輸出; Kij、bij分別為對應直線的斜率和偏置常數為使a和b光敏元的轉換特性經校正后均表現為直線c所表示的轉換關系,按以下2式選擇斜率校正系數Gij和偏置校正系數Cij.

?
式(2)中, Kc為常數, 表示直線c的斜率. 對Kc的選擇具有很強的隨意性, 通常選取所有光敏元中最大斜率的光電轉換直線或者取過2個不同光照下各個光敏元的算術平均值的直線作為標準. 筆者則以獲取盡可能大的Gij作為標準, 因此, 由Gij (最大取值可為250)和(Ui(j+1) - Uij )值可確定(Uc(j+1) - Ucj )值的范圍,從而確定Kc值. 同時保證校正后的視頻輸出值在飽和輻照度范圍內隨輻照度增強而增大.
式(3)中,Mj為常數. 在保證光電轉換曲線分段線性化后的連續性和單值性的情況下,Mj值等于分段點Hj校正后的視頻電壓值. 同時, 結合Uij以及選擇合適的Gij ,保證獲取盡可能大Cij. 因此,校正后的視頻輸出Uc可表示為
?
將式(1) 、式(2)和式(3)代入式(4) ,經整理后得:
?
可見,因為Kc、Mj和Hj均為常數, 經過校正處理后, 在同一輻照度下, 2個光敏元都有相同的視頻輸出電壓并且輸出電壓值與輻照度大小成一一對應的線性關系. 同理,對有m 個光敏元的傳感器采用上述校正原理和校正算法可實現其非均勻性校正.
此外,由于不同圖像傳感器的光電轉換曲線各不相同,所以,在輻照度區域的劃分時,各邊界點應根據具體傳感器的特性加以選擇,不能一概而論. 筆者所采取的選取原則是,采用實驗測取數據,擬合出曲線的大致變化情況,再進行輻照度區域劃分.
 電子發燒友App
電子發燒友App




















評論