在科學(xué)計算中，需要大量的矩陣運算，而矩陣運算中乘法運算是其他運算的基礎(chǔ)，如能提高嵌入式系統(tǒng)中浮點矩陣乘法運算的速度，則可加快其他類型的矩陣運算速度。

　　目前實現(xiàn)浮點矩陣運算的方法，有直接使用VHDL語言編寫的浮點矩陣相乘處理單元[1]，關(guān)鍵技術(shù)是乘累加單元的設(shè)計，通常依據(jù)設(shè)計者的編程水平?jīng)Q定硬件性能。同樣，FPGA廠商也推出了一定規(guī)模的浮點矩陣運算IP核[2]，其應(yīng)用針對本廠家器件，且經(jīng)過專業(yè)調(diào)試和硬件實測，性能穩(wěn)定且優(yōu)于手寫代碼，但還有一些可改進的地方。

　　本文基于Altera的算法IP核，采用數(shù)選方式對矩陣運算中的單精度浮點矩陣相乘進行改進，可推廣到階數(shù)更高的矩陣運算和雙精度浮點、復(fù)數(shù)單精度浮點運算中。

　　1 浮點矩陣相乘的IP核原理

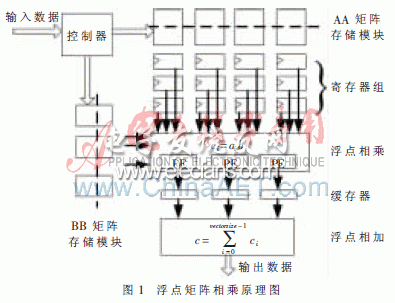
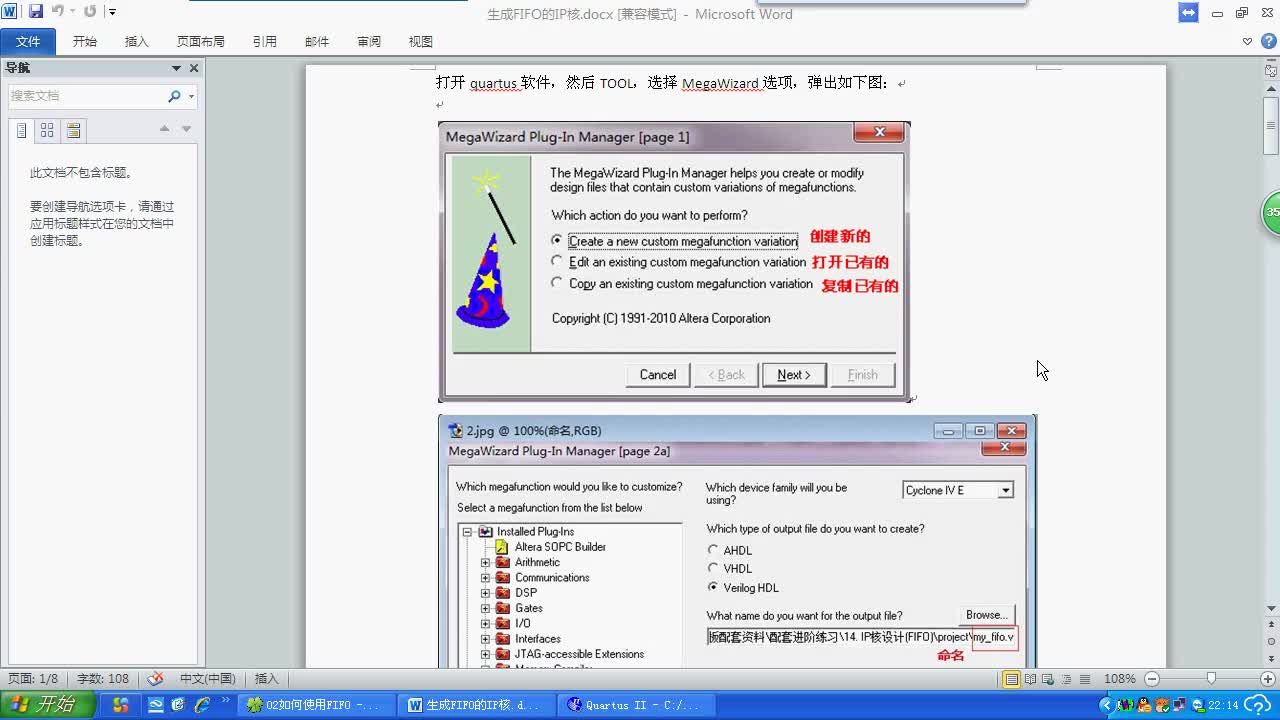
　　Altera公司推出的浮點矩陣相乘IP核ALTFP_MATRIX_MULT，適用于Quartus10.1版本以上的軟件環(huán)境，能夠進行一定規(guī)模的浮點矩陣計算，原理圖如圖1所示。

?

　　圖1的矩陣相乘結(jié)合流水線方式控制數(shù)據(jù)流動，關(guān)鍵部分為核心PE(Processing Element)單元實現(xiàn)兩浮點數(shù)的相乘。輸入數(shù)據(jù)在控制器的引導(dǎo)下分為AA矩陣和BB矩陣，分別存于M144K或M9K存儲器中，在計算指令的控制下做浮點相乘運算，接著并行地浮點相加完成輸出。分析整個計算結(jié)構(gòu)，要達到較好的性能就需要耗費多個存儲器和多個浮點相乘單元。列出矩陣相乘的基本時序圖如圖2所示。

?

　　從時序圖可見，整個IP核有7個輸入、4個輸出，分為數(shù)據(jù)加載、數(shù)據(jù)處理、數(shù)據(jù)輸出三個階段。在系統(tǒng)同步時鐘sysclk的驅(qū)動下，loadaa、loadbb對數(shù)據(jù)loaddata進行乘數(shù)矩陣、被乘數(shù)矩陣使能，將數(shù)據(jù)加載到存儲器中。當calcimatrix上升沿到來時，進行矩陣乘法運算并輸出數(shù)據(jù)outdata，且在outvalid為高電平時有效。在整個數(shù)據(jù)輸出有效階段，完成信號done處于低電平，其余階段為高電平。

　　浮點矩陣運算IP核的運算方式分為單精度、雙精度、復(fù)數(shù)單精度三種方式，矩陣運算階數(shù)有8、16、32、64、96、128階6種，并不能實現(xiàn)任意階矩陣的相乘，隨著矩陣階數(shù)的增大，最高時鐘頻率在下降，同時占用器件資源在增加，耗用最多的是存儲器資源，呈幾何倍數(shù)增長。

　　2 數(shù)選實矩陣相乘設(shè)計

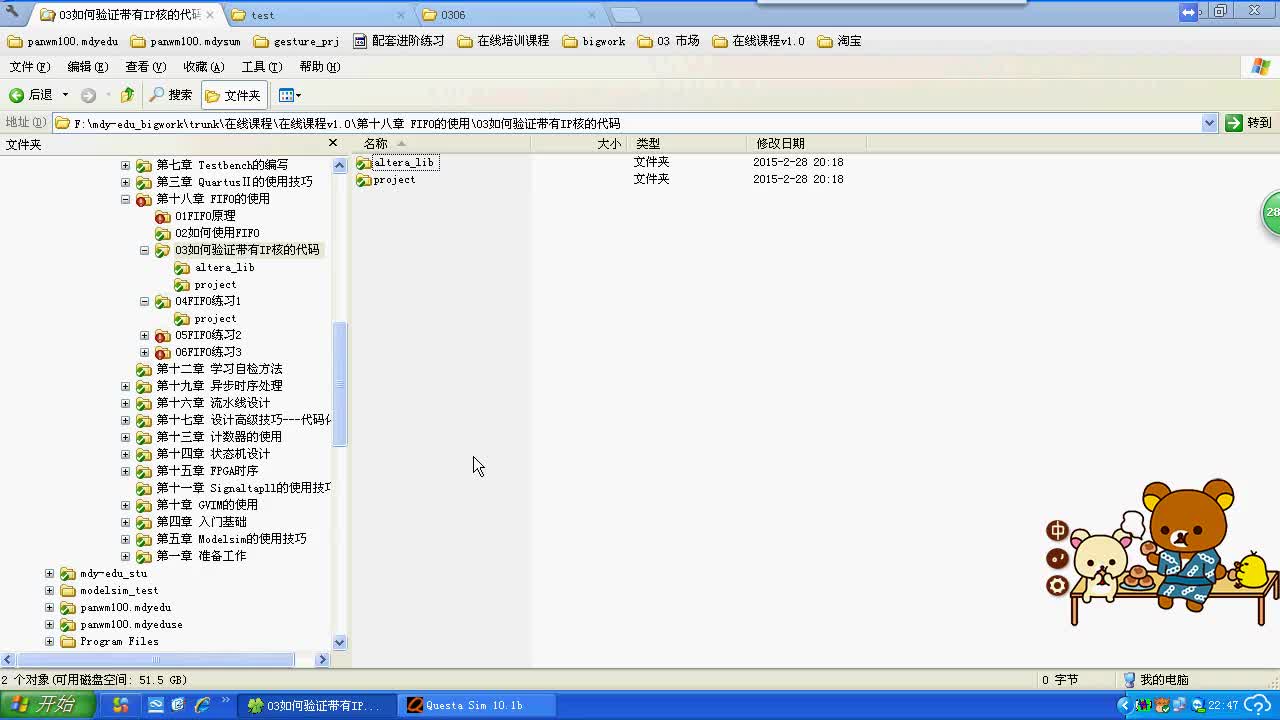
　　在矩陣相乘運算中最基礎(chǔ)的是2階矩陣的相乘，核心部分為乘累加器[3]，通過適當數(shù)選控制，可使整個矩陣運算具有高時鐘頻率。如圖3為2階矩陣相乘電路。

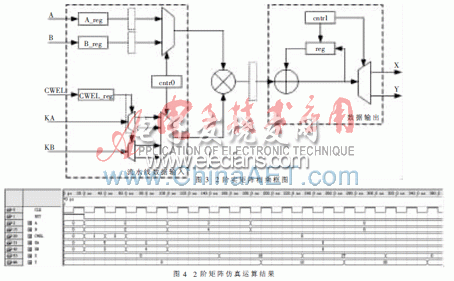
　　整個矩陣相乘模塊的設(shè)計，結(jié)合數(shù)據(jù)選擇的控制方式，分為流水線數(shù)據(jù)輸入、數(shù)據(jù)相乘、數(shù)據(jù)輸出三部分。在流水線數(shù)據(jù)輸入模塊，采用流水線的方式輸入乘矩陣數(shù)據(jù)KA、KB，被乘數(shù)矩陣數(shù)據(jù)A、B，以同步系統(tǒng)時鐘啟動兩個數(shù)據(jù)選擇器，由cntr0控制兩個數(shù)選器選擇數(shù)據(jù)輸出到乘法器兩端;將乘法器的輸入數(shù)據(jù)相乘并存于寄存器中;最后在數(shù)據(jù)輸出部分cntr1模塊的控制下，累加輸出矩陣數(shù)據(jù)X、Y，完成矩陣運算。以Altera器件EP2C35F672C6為映射器件，其時鐘頻率為250 MHz。在Quartus7.2軟件編程下，運行此2階乘法器，可獲得248.69 MHz的最高時鐘頻率。占用資源為172個邏輯單元、152個寄存器、2個9位乘法器，且在輸入數(shù)據(jù)之后2個時鐘輸出運算結(jié)果，如圖4所示。設(shè)計具有較高的計算性能，關(guān)鍵點在于數(shù)據(jù)選擇器在電路運算過程中的作用，取代了存儲器單一存儲的目的，可進行乒乓式實時數(shù)據(jù)流動，提高系統(tǒng)運算效率，節(jié)省了一半存儲器。

　　圖4中乘矩陣[KA KB]在Matlab中的表示為[5 3;2 4]，被乘矩陣[A B]表示為[2 2;3 4]，得到的輸出結(jié)果為[16 27;12 22]，可見FPGA運算結(jié)果與Matlab結(jié)果一致。

?

　　3 浮點矩陣相乘運算的改進

　　本文以16×16階浮點矩陣相乘為例，采用單精度浮點計算方式，結(jié)合2階高速矩陣運算電路對16階矩陣運算進行改進，其他高階矩陣運算可采用類推的方式完成。

　　3.1 高階矩陣運算分解

　　高階矩陣分解運算是通過分解大規(guī)模矩陣為許多子矩陣進行計算的方式，所以可將16×16階矩陣劃分為4個8×8階矩陣，實現(xiàn)2階矩陣相乘。16×16階矩陣相乘運算，可表達為式(1)：

?

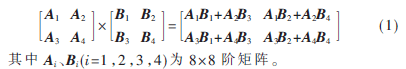
　　從式(1)的16階矩陣相乘運算，可知其需要8次8階浮點矩陣相乘和4次8階浮點矩陣相加運算。分析可得，在數(shù)據(jù)并行輸入輸出的情況下，相比較于16階矩陣IP核的運行方式，此種分解方式性能要高。主要由于IP核運行方式跨度長，在數(shù)據(jù)輸入時，需要經(jīng)過16×16級存儲器，而本文設(shè)計的方式只需要8×8級存儲和4次并行的浮點相加運算，同時相比較于16階IP耗用存儲資源和浮點乘法單元數(shù)較少。

　　3.2 矩陣相乘硬件實現(xiàn)

　　采用Quartus10.1軟件設(shè)計16階單精度浮點矩陣相乘電路，使用VHDL語言[4]編寫，模塊由流水線數(shù)據(jù)輸入、矩陣相乘、鎖存器、浮點加法數(shù)選模塊4部分組成，設(shè)計框圖如圖5所示。

　　在流水線數(shù)據(jù)輸入部分，對數(shù)據(jù)data進行分割，當信號load為高電平時使能，同時進行數(shù)據(jù)的緩存和生成控制位，輸出的三位控制位(calcimatrix、loadaa、loadbb)控制著下一步矩陣相乘的運算，在loadaa與loadbb高電平交互之間的數(shù)據(jù)值取0，具有數(shù)據(jù)緩存和分割的作用。最后一個模塊需要進行8×8階矩陣的32位浮點加法運算，同時輸出數(shù)據(jù)有效電平，使用Altera altfp_add_sub IP 核實現(xiàn)單精度浮點加法器，可根據(jù)用戶的定制完成。對圖5的模塊加入幾個輸出結(jié)果，使用modelsim6.5進行仿真，可得16階矩陣運算仿真結(jié)果如圖6所示。

?

　　從圖6可見loadaa、loadbb、calcimatrix三者的時序滿足浮點矩陣運算的時序圖，在前兩者數(shù)據(jù)加載后，即可獲得calcimatrix上升沿，進行矩陣相乘。輸出結(jié)果分為4個大組，各大組有8小組，每一小組由8個數(shù)據(jù)組成，具有較好的計算結(jié)果。

　　4 性能比較分析

　　4.1 性能比較

　　將第3節(jié)設(shè)計的16階矩陣相乘電路與Altera自身提供的IP核進行比較。同時以8階矩陣相乘為基，以第2節(jié)的方式設(shè)計4×4階數(shù)選實矩陣電路，套用于32×32階矩陣運算中，與Altera的IP核比較。IP核使用最高性能運行，同時以資源消耗、浮點操作數(shù)[5]、最高時鐘頻率、吞吐量作為比較準則，其中浮點操作數(shù)的計算表達式為：

?

　　依據(jù)以上浮點操作數(shù)計算方式，使用Quartus10.1軟件進行編程，映射到Stratix III系列的器件中，可獲得相應(yīng)的對比表如表1所示。

?

　　從表1結(jié)果可見改進的浮點運算電路在ALM的資源占用減少了許多。原因為在矩陣規(guī)模增大時，只使用了8階浮點矩陣運算，浮點IP核中的乘加核數(shù)量不變，所以消耗的浮點相乘單元不變，同樣增添的浮點加法器也只消耗了不多的ALM資源。而對于改進的兩類矩陣相乘都只使用8階矩陣乘法，所以在乘法器和M9K存儲器這兩類邏輯單元的消耗不變。為了達到較好的性能，需要少量外圍存儲器處理數(shù)據(jù)的流動和浮點相加運算，但整體存儲器消耗降低。觀察吞吐量可知，套用的數(shù)選式矩陣相乘模塊，當階數(shù)增大時吞吐量降低，幅度明顯，而選擇2階數(shù)選矩陣具有乒乓結(jié)構(gòu)，性能有所提升。同理適用于浮點操作數(shù)的情況。最后整個運算電路的最高時鐘頻率始終是提升的。與Altera公司的IP核比較，改進的16階浮點矩陣運算電路性能較好，而32階運算電路性能卻未達到要求。

　　對高階矩陣進一步分析，在32階運算電路的設(shè)計中，使用16階浮點矩陣為乘法運算部分，以2×2實矩陣運算電路為核心，能夠提升32階電路的運算性能。

　　4.2 精度分析

　　以16階矩陣的運算進行精度分析，取乘矩陣與被乘矩陣各16個數(shù)據(jù)進行計算分析，列出表2數(shù)據(jù)，其中B矩陣為現(xiàn)有數(shù)據(jù)的轉(zhuǎn)置，以Matlab和FPGA運算結(jié)果進行對比。

?

　　從Matlab與FPGA計算結(jié)果可見，計算輸出近乎完全相同，相差的數(shù)據(jù)值也是由于Matlab在計算中需要先轉(zhuǎn)化為雙精度運算后才轉(zhuǎn)化為單精度數(shù)，從而得出FPGA計算具有較高的精度。

　　本設(shè)計降低存儲器和計算資源消耗，提升了系統(tǒng)吞吐量、浮點運算性能和運行最高時鐘頻率。這種改進的浮點矩陣乘法器對降低資源消耗、提升系統(tǒng)性能具有重大意義。同時，利用VHDL語言編寫，具有模塊化設(shè)計思想，使得本設(shè)計可移植性強、通用性好，只需要在現(xiàn)有IP核的基礎(chǔ)上進行小規(guī)模改進，即可擁有較高性能，具有一定的工程實際意義和應(yīng)用前景。