三角函數的計算是個復雜的主題，有計算機之前，人們通常通過查找三角函數表來計算任意角度的三角函數的值。這種表格在人們剛剛產生三角函數的概念的時候就已經有了，它們通常是通過從已知值（比如sin(π/2)=1）開始并重復應用半角和和差公式而生成。

現在有了計算機，三角函數表便推出了歷史的舞臺。但是像我這樣的喜歡刨根問底的人，不禁要問計算機又是如何計算三角函數值的呢。最容易想到的辦法就是利用級數展開，比如泰勒級數來逼近三角函數，只要項數取得足夠多就能以任意的精度來逼近函數值。除了泰勒級數逼近之外，還有其他許多的逼近方法，比如切比雪夫逼近、最佳一致逼近和Padé逼近等。

所有這些逼近方法本質上都是用多項式函數來近似我們要計算的三角函數，計算過程中必然要涉及到大量的浮點運算。在缺乏硬件乘法器的簡單設備上（比如沒有浮點運算單元的單片機），用這些方法來計算三角函數會非常的費時。為了解決這個問題，J. Volder于1959年提出了一種快速算法，稱之為CORDIC(COordinate Rotation DIgital Computer) 算法，這個算法只利用移位和加減運算，就能計算常用三角函數值，如Sin，Cos，Sinh，Cosh等函數。 J. Walther在1974年在這種算法的基礎上進一步改進，使其可以計算出多種超越函數，更大的擴展了Cordic 算法的應用。因為Cordic 算法只用了移位和加法，很容易用純硬件來實現，因此我們常能在FPGA運算平臺上見到它的身影。不過，大多數的軟件程序員們都沒有聽說過這種算法，也更不會主動的去用這種算法。其實，在嵌入式軟件開發，尤其是在沒有浮點運算指令的嵌入式平臺（比如定點型DSP）上做開發時，還是會遇上可以用到Cordic 算法的情況的，所以掌握基本的Cordic算法還是有用的。

從二分查找法說起
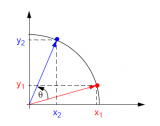
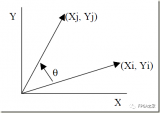
先從一個例子說起，知道平面上一點在直角坐標系下的坐標（X,Y）=（100，200），如何求的在極坐標系下的坐標（ρ,θ）。用計算器計算一下可知答案是（223.61，63.435）。

圖 1 直角坐標系到極坐標系的轉換

?

可能有讀者會問，計算中用到了 sin 函數和 cos 函數，這些值又是怎么計算呢。很簡單，我們只用到很少的幾個特殊點的sin 函數和 cos 函數的值，提前計算好存起來，用時查表。

下面給出上面方法的C 語言實現。
? ? ? ?
#include
#include?

double my_atan2(double x, double y);
int main(void)
{
double z = my_atan2(100.0, 200.0);
printf("\n z = %f \n", z);

return 0;
}

double my_atan2(double x, double y)
{
const double sine[] = {0.7071067811865,0.3826834323651,0.1950903220161,0.09801714032956,
0.04906767432742,0.02454122852291,0.01227153828572,0.006135884649154,0.003067956762966
,0.001533980186285,7.669903187427045e-4,3.834951875713956e-4,1.917475973107033e-4,
9.587379909597735e-5,4.793689960306688e-5,2.396844980841822e-5
};

const double cosine[] = {0.7071067811865,0.9238795325113,0.9807852804032,0.9951847266722,
0.9987954562052,0.9996988186962,0.9999247018391,0.9999811752826,0.9999952938096,
0.9999988234517,0.9999997058629,0.9999999264657,0.9999999816164,0.9999999954041,
0.999999998851,0.9999999997128
};

int i = 0;
double x_new, y_new;
double angleSum = 0.0;
double angle = 45.0;

for(i = 0; i < 15; i++)
{
if(y > 0)
{
x_new = x * cosine[i] + y * sine[i];
y_new = y * cosine[i] - x * sine[i];
x = x_new;
y = y_new;
angleSum += angle;
}
else
{
x_new = x * cosine[i] - y * sine[i];
y_new = y * cosine[i] + x * sine[i];
x = x_new;
y = y_new;
angleSum -= angle;
}
printf("Debug: i = %d angleSum = %f, angle = %f\n", i, angleSum, angle);
angle /= 2;
}
return angleSum;
}

程序運行的輸出結果如下：
Debug: i = 0 angleSum = 45.000000, angle = 45.000000
Debug: i = 1 angleSum = 67.500000, angle = 22.500000
Debug: i = 2 angleSum = 56.250000, angle = 11.250000
Debug: i = 3 angleSum = 61.875000, angle = 5.625000
Debug: i = 4 angleSum = 64.687500, angle = 2.812500
Debug: i = 5 angleSum = 63.281250, angle = 1.406250
Debug: i = 6 angleSum = 63.984375, angle = 0.703125
Debug: i = 7 angleSum = 63.632813, angle = 0.351563
Debug: i = 8 angleSum = 63.457031, angle = 0.175781
Debug: i = 9 angleSum = 63.369141, angle = 0.087891
Debug: i = 10 angleSum = 63.413086, angle = 0.043945
Debug: i = 11 angleSum = 63.435059, angle = 0.021973
Debug: i = 12 angleSum = 63.424072, angle = 0.010986
Debug: i = 13 angleSum = 63.429565, angle = 0.005493
Debug: i = 14 angleSum = 63.432312, angle = 0.002747

z = 63.432312

減少乘法運算
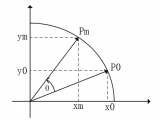
現在已經有點 Cordic 算法的樣子了，但是我們看到沒次循環都要計算 4 次浮點數的乘法運算，運算量還是太大了。還需要進一步的改進。改進的切入點當然還是坐標變換的過程。我們將坐標變換公式變一下形。

?

可以看出 cos(θ)可以從矩陣運算中提出來。我們可以做的再徹底些，直接把 cos(θ) 給省略掉。

省略cos(θ)后發生了什么呢，每次旋轉后的新坐標點到原點的距離都變長了，放縮的系數是1/cos(θ)。不過沒有關系，我們求的是θ，不關心ρ的改變。這樣的變形非常的簡單，但是每次循環的運算量一下就從4次乘法降到了2次乘法了。

還是給出 C 語言的實現：
double my_atan3(double x, double y)
{
const double tangent[] = {1.0,0.4142135623731,0.1989123673797,0.09849140335716,0.04912684976947,
0.02454862210893,0.01227246237957,0.006136000157623,0.003067971201423,
0.001533981991089,7.669905443430926e-4,3.83495215771441e-4,1.917476008357089e-4,
9.587379953660303e-5,4.79368996581451e-5,2.3968449815303e-5
};

int i = 0;
double x_new, y_new;
double angleSum = 0.0;
double angle = 45.0;

for(i = 0; i < 15; i++)
{
if(y > 0)
{
x_new = x + y * tangent[i];
y_new = y - x * tangent[i];
x = x_new;
y = y_new;
angleSum += angle;
}
else
{
x_new = x - y * tangent[i];
y_new = y + x * tangent[i];
x = x_new;
y = y_new;
angleSum -= angle;
}
printf("Debug: i = %d angleSum = %f, angle = %f, ρ = %f\n", i, angleSum, angle, hypot(x,y));
angle /= 2;
}
return angleSum;
}

計算的結果是：
Debug: i = 0 angleSum = 45.000000, angle = 45.000000, ρ = 316.227766
Debug: i = 1 angleSum = 67.500000, angle = 22.500000, ρ = 342.282467
Debug: i = 2 angleSum = 56.250000, angle = 11.250000, ρ = 348.988177
Debug: i = 3 angleSum = 61.875000, angle = 5.625000, ρ = 350.676782
Debug: i = 4 angleSum = 64.687500, angle = 2.812500, ρ = 351.099697
Debug: i = 5 angleSum = 63.281250, angle = 1.406250, ρ = 351.205473
Debug: i = 6 angleSum = 63.984375, angle = 0.703125, ρ = 351.231921
Debug: i = 7 angleSum = 63.632813, angle = 0.351563, ρ = 351.238533
Debug: i = 8 angleSum = 63.457031, angle = 0.175781, ρ = 351.240186
Debug: i = 9 angleSum = 63.369141, angle = 0.087891, ρ = 351.240599
Debug: i = 10 angleSum = 63.413086, angle = 0.043945, ρ = 351.240702
Debug: i = 11 angleSum = 63.435059, angle = 0.021973, ρ = 351.240728
Debug: i = 12 angleSum = 63.424072, angle = 0.010986, ρ = 351.240734
Debug: i = 13 angleSum = 63.429565, angle = 0.005493, ρ = 351.240736
Debug: i = 14 angleSum = 63.432312, angle = 0.002747, ρ = 351.240736

z = 63.432312

消除乘法運算
我們已經成功的將乘法的次數減少了一半，還有沒有可能進一步降低運算量呢？還要從計算式入手。

第一次循環時，tan(45)=1，所以第一次循環實際上是不需要乘法運算的。第二次運算呢？
Tan(22.5)=0.4142135623731,很不幸，第二次循環乘數是個很不整的小數。是否能對其改造一下呢？答案是肯定的。第二次選擇22.5度是因為二分查找法的查找效率最高。如果選用個在22.5到45度之間的值，查找的效率會降低一些。如果稍微降低一點查找的效率能讓我們有效的減少乘法的次數，使最終的計算速度提高了，那么這種改進就是值得的。

我們發現tan(26.565051177078)=0.5，如果我們第二次旋轉采用26.565051177078度，那么乘數變為0.5，如果我們采用定點數運算的話（沒有浮點協處理器時為了加速計算我們會大量的采用定點數算法）乘以0.5就相當于將乘數右移一位。右移運算是很快的，這樣第二次循環中的乘法運算也被消除了。

類似的方法，第三次循環中不用11.25度，而采用 14.0362434679265 度。
Tan(14.0362434679265)= 1/4

乘數右移兩位就可以了。剩下的都以此類推。
tan(45)= 1
tan(26.565051177078)= 1/2
tan(14.0362434679265)= 1/4
tan(7.1250163489018)= 1/8
tan(3.57633437499735)= 1/16
tan(1.78991060824607)= 1/32
tan(0.8951737102111)= 1/64
tan(0.4476141708606)= 1/128
tan(0.2238105003685)= 1/256

還是給出C語言的實現代碼，我們采用循序漸進的方法，先給出浮點數的實現（因為用到了浮點數，所以并沒有減少乘法運算量，查找的效率也比二分查找法要低，理論上說這個算法實現很低效。不過這個代碼的目的在于給出算法實現的示意性說明，還是有意義的）。
double my_atan4(double x, double y)
{
const double tangent[] = {1.0, 1 / 2.0, 1 / 4.0, 1 / 8.0, 1 / 16.0,
1 / 32.0, 1 / 64.0, 1 / 128.0, 1 / 256.0, 1 / 512.0,
1 / 1024.0, 1 / 2048.0, 1 / 4096.0, 1 / 8192.0, 1 / 16384.0
};
const double angle[] = {45.0, 26.565051177078, 14.0362434679265, 7.1250163489018, 3.57633437499735,
1.78991060824607, 0.8951737102111, 0.4476141708606, 0.2238105003685, 0.1119056770662,
0.0559528918938, 0.027976452617, 0.01398822714227, 0.006994113675353, 0.003497056850704
};

int i = 0;
double x_new, y_new;
double angleSum = 0.0;

for(i = 0; i < 15; i++)
{
if(y > 0)
{
x_new = x + y * tangent[i];
y_new = y - x * tangent[i];
x = x_new;
y = y_new;
angleSum += angle[i];
}
else
{
x_new = x - y * tangent[i];
y_new = y + x * tangent[i];
x = x_new;
y = y_new;
angleSum -= angle[i];
}
printf("Debug: i = %d angleSum = %f, angle = %f, ρ = %f\n", i, angleSum, angle[i], hypot(x, y));
}
return angleSum;
}

程序運行的輸出結果如下：
Debug: i = 0 angleSum = 45.000000, angle = 45.000000, ρ = 316.227766
Debug: i = 1 angleSum = 71.565051, angle = 26.565051, ρ = 353.553391
Debug: i = 2 angleSum = 57.528808, angle = 14.036243, ρ = 364.434493
Debug: i = 3 angleSum = 64.653824, angle = 7.125016, ρ = 367.270602
Debug: i = 4 angleSum = 61.077490, angle = 3.576334, ρ = 367.987229
Debug: i = 5 angleSum = 62.867400, angle = 1.789911, ρ = 368.166866
Debug: i = 6 angleSum = 63.762574, angle = 0.895174, ρ = 368.211805
Debug: i = 7 angleSum = 63.314960, angle = 0.447614, ρ = 368.223042
Debug: i = 8 angleSum = 63.538770, angle = 0.223811, ρ = 368.225852
Debug: i = 9 angleSum = 63.426865, angle = 0.111906, ρ = 368.226554
Debug: i = 10 angleSum = 63.482818, angle = 0.055953, ρ = 368.226729
Debug: i = 11 angleSum = 63.454841, angle = 0.027976, ρ = 368.226773
Debug: i = 12 angleSum = 63.440853, angle = 0.013988, ρ = 368.226784
Debug: i = 13 angleSum = 63.433859, angle = 0.006994, ρ = 368.226787
Debug: i = 14 angleSum = 63.437356, angle = 0.003497, ρ = 368.226788

z = 63.437356

定點數算法e#

有了上面的準備，我們可以來討論定點數算法了。所謂定點數運算，其實就是整數運算。我們用256 表示1度。這樣的話我們就可以精確到1/256=0.00390625 度了，這對于大多數的情況都是足夠精確的了。256 表示1度，那么45度就是 45*256 = 115200。其他的度數以此類推。

?

序號

?

度數

?

×256

?

取整

?

1

?

45.0

?

11520

?

11520

?

2

?

26.565051177078

?

6800.65310133196

?

6801

?

3

?

14.0362434679265

?

3593.27832778918

?

3593

?

4

?

7.1250163489018

?

1824.00418531886

?

1824

?

5

?

3.57633437499735

?

915.541599999322

?

916

?

6

?

1.78991060824607

?

458.217115710994

?

458

?

7

?

0.8951737102111

?

229.164469814035

?

229

?

8

?

0.4476141708606

?

114.589227740302

?

115

?

9

?

0.2238105003685

?

57.2954880943458

?

57

?

10

?

0.1119056770662

?

28.647853328949

?

29

?

11

?

0.0559528918938

?

14.3239403248137

?

14

?

12

?

0.027976452617

?

7.16197186995294

?

7

?

13

?

0.01398822714227

?

3.58098614841984

?

4

?

14

?

0.006994113675353

?

1.79049310089035

?

2

?

15

?

0.003497056850704

?

0.8952465537802

?

1

?

?

C 代碼如下：
int my_atan5(int x, int y)
{
const int angle[] = {11520, 6801, 3593, 1824, 916, 458, 229, 115, 57, 29, 14, 7, 4, 2, 1};

int i = 0;
int x_new, y_new;
int angleSum = 0;

x *= 1024;// 將 X Y 放大一些，結果會更準確
y *= 1024;

for(i = 0; i < 15; i++)
{
if(y > 0)
{
x_new = x + (y >> i);
y_new = y - (x >> i);
x = x_new;
y = y_new;
angleSum += angle[i];
}
else
{
x_new = x - (y >> i);
y_new = y + (x >> i);
x = x_new;
y = y_new;
angleSum -= angle[i];
}
printf("Debug: i = %d angleSum = %d, angle = %d\n", i, angleSum, angle[i]);
}
return angleSum;
}

計算結果如下：
Debug: i = 0 angleSum = 11520, angle = 11520
Debug: i = 1 angleSum = 18321, angle = 6801
Debug: i = 2 angleSum = 14728, angle = 3593
Debug: i = 3 angleSum = 16552, angle = 1824
Debug: i = 4 angleSum = 15636, angle = 916
Debug: i = 5 angleSum = 16094, angle = 458
Debug: i = 6 angleSum = 16323, angle = 229
Debug: i = 7 angleSum = 16208, angle = 115
Debug: i = 8 angleSum = 16265, angle = 57
Debug: i = 9 angleSum = 16236, angle = 29
Debug: i = 10 angleSum = 16250, angle = 14
Debug: i = 11 angleSum = 16243, angle = 7
Debug: i = 12 angleSum = 16239, angle = 4
Debug: i = 13 angleSum = 16237, angle = 2
Debug: i = 14 angleSum = 16238, angle = 1

z = 16238

16238/256=63.4296875度，精確的結果是63.4349499度，兩個結果的差為0.00526，還是很精確的。
到這里 CORDIC 算法的最核心的思想就介紹完了。當然，這里介紹的只是CORDIC算法最基本的內容，實際上，利用CORDIC 算法不光可以計算 atan 函數，其他的像 Sin，Cos，Sinh，Cosh 等一系列的函數都可以計算，不過那些都不在本文的討論范圍內了。另外，每次旋轉時到原點的距離都會發生變化，而這個變化是確定的，因此可以在循環運算結束后以此補償回來，這樣的話我們就同時將（ρ,θ）都計算出來了。

想進一步深入學習的可以閱讀 John Stephen Walther 于2000年發表在 Journal of VLSI signal processing systems for signal, image and video technology上的綜述性文章“The Story of Unified Cordic”。