為了得到最小的噪聲系數, 源阻抗最佳值(最佳噪聲源阻抗) Zop t應滿足：

其中,α為共源管跨導與其源漏電導的比值。δ為一常數,γ為一系數, 在長溝道器件中,δ的值約為1. 33,γ的值約為0. 67, 在短溝道器件中, 這兩個值都會因為短溝道效應而變大。定義c為柵噪聲與漏噪聲相關系數, 其值一般為0. 395 j, 為一純虛數,反映了柵和溝道間噪聲引起的的容性耦合程度。

源級電感Ls 和柵極電感Lg 不會導致最佳噪聲源阻抗的實部發生變化,而僅對電抗部分產生影響。

要實現功率和噪聲同時匹配,必須使輸入阻抗Zin和最佳噪聲源阻抗Zop t共軛匹配, 令Zin = 50 Ω,則有：

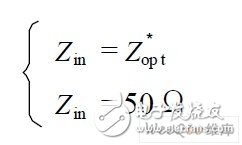
即：

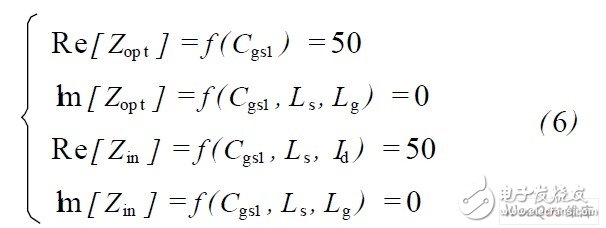
式(6)中有4個方程, 4個未知數,只有一組解,即功率匹配和噪聲匹配同時滿足時, 功耗( Id )是確定的,不可以優化。而在限定功耗的情況下,功率匹配和噪聲匹配則不可能同時滿足。

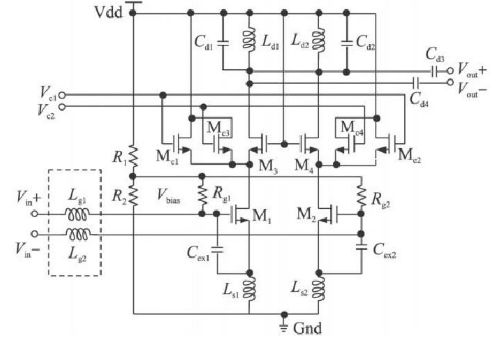
于是在電路設計中就需要在噪聲匹配和功率匹配中進行折中。下面引入M1 管柵源間附加電容Cex ,這樣,輸入阻抗變為：

最佳噪聲阻抗Z ′ op t表示為：

這樣, 為了使功率和噪聲同時匹配, 令Zin =Z ′ op t*= 50Ω,得到：

式( 9)中有4個方程, 5個未知數,則可以限定任何一個參數,再優化其它參數。所以,在功耗( Id )限定的情況下, 仍然可以進行功率噪聲匹配。引入Cex后,通過調整Cex ,首先可以使最佳噪聲源阻抗Z ′op t實部為50Ω。

再選擇Ls ,使電路滿足Re [ Z′in ] = Re [ Z ′op t ] =50Ω。根據式(8) 、式(9)可以推出：

式(10)指出,選取的Ls 的電感值在引入Cex后亦可以比沒有連接Cex時有所降低。Ls 為源極負反饋電感,由于電感中的寄生電阻影響以及該電感本身的負反饋性質,低感值的電感可以做到更好的噪聲系數。

最后,調整片外電感Lg ,使諧振頻率為ω0 (設計要求ω0 為2. 43 GHz) ,ω0 表示為：

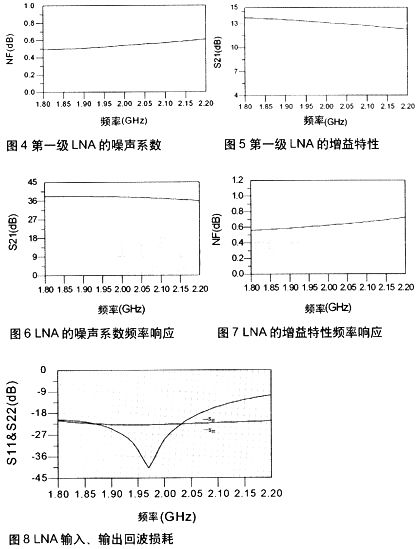
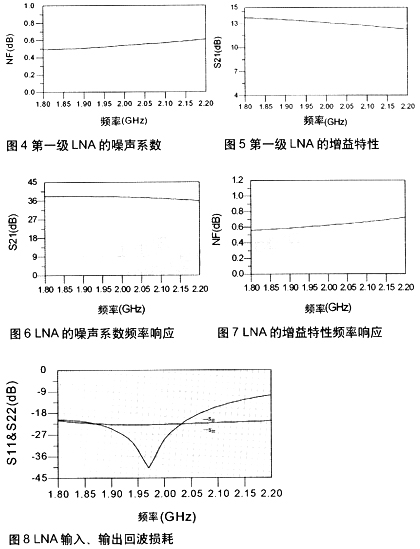
由于Cadence工具的局限性,仿真S參數時無法顯示Sop t曲線,噪聲匹配很難做到最優。在實際設計過程中,當共源管M1、M2 寬長比以及其偏置電路都已經確定時,可以通過掃描Cex參數,比較最小噪聲系數NFmin ,選取其最佳值。當最小噪聲系數NFmin確定后,再通過進一步調整Cex ,盡量滿足功率匹配。在此過程中,必須同時關注噪聲系數NF和最小噪聲系數NFmin的變化,最后通過比較,選擇折中的優化結果,確定恰當的Cex和Ls、Lg 值。

1. 3　輸出匹配

電路輸出端通過漏極電感并聯、串聯電容的結構實現阻抗匹配。漏極電感的選取對低噪聲放大器的性能有較大影響。電感值的大小直接影響放大器的增益。較大感值的電感可以增加LC并聯諧振電路的等效阻抗,從而帶來更高的電壓增益。但是大電感的自諧振頻率較低,而射頻電路要求的工作頻率卻很高。同時,大電感也會占用更大的芯片面積,引入較大的噪聲。而且,當電感值過大使放大器輸出阻抗實部超過50Ω時,必需通過在輸出端并聯電感或增加源極跟隨器等緩沖電路的方法才能將輸出阻抗匹配到50Ω。如果直接并聯電感,則會使輸出端直流短路,要解決這個問題,則必須串聯一個大電容后再將此電感并入電路,對于整體設計來說,引入了更多的無源元件,一方面大大影響了電路性能,另一方面也占用了更多面積。而增加一級緩沖電路,則會增加放大器的額外功耗。對于無線傳感器網絡節點中的模塊,這兩種方法都不可行。因此,具體設計時,需選取恰當的電感,既能保證應有的增益,又可以使輸出阻抗實部在50Ω附近。