圖像分割的實現(xiàn)
我用了Roberts算子、Sobel算子和Kirsh算子邊緣檢測的方法但都由于亮度不均等因素對圖像分割的效果不太好:
Sobel:
void sobel (unsignedchar* des, constunsignedchar* src, int width, int height)
{
for (int y=0; y《height; y++)
for (int x=0; x《width; x++)
des[y * width + x]=255;
/* Now compute the convolution, scaling */
for (int y=1; y《height-1; y++)
for (int x=1; x《width-1; x++)
{
double n = (src[(y+1)*width+x-1]+2*src[(y+1)*width+x]+src[(y+1)*width+x+1]) -
(src[(y-1)*width+x-1]+2*src[(y-1)*width+x]+src[(y-1)*width+x+1]);
double m = (src[(y-1)*width+x+1]+2*src[y*width+x+1]+src[(y+1)*width+x+1])-
(src[(y-1)*width+x-1]+2*src[y*width+x-1]+src[(y+1)*width+x-1]);
double k = (int)( sqrt( (double)(n*n + m*m) )/4.0 );
des[y * width + x] = k;
}
thresh (des, width,height);
}
Roberts算子:
void roberts(unsignedchar* des, constunsignedchar* src, int width, int height)
{
for (int y=0; y《height; y++)
for (int x=0; x《width; x++)
des[y * width + x]=255;
/* Now compute the convolution, scaling */
for (int y=1; y《height-1; y++)
for (int x=1; x《width-1; x++)
{
double n = src[y*width+x] - src[(y+1)*width+x+1];
double m = src[(y+1)*width+x] - src[y*width+x+1];
double k = abs(m)+abs(n);
des[y * width + x] = k;
}
thresh (des, width,height);
}
Kirsch算子:
void kirsch(unsigned char* des, const unsigned char* src, int width, int height)
{
// TODO: Add your command handler code here
//顯示數(shù)值
long int i,j,Ns;
static int nWeight[8][3][3];//對一個靜態(tài)整型數(shù)組賦初值,模板
double dGrad[8];
int nTmp[3][3],xx,yy;//每像素點的鄰域值
nWeight[0][0][0] = -1 ;
nWeight[0][0][1] = 0 ;
nWeight[0][0][2] = 1 ;
nWeight[0][1][0] = -2 ;
nWeight[0][1][1] = 0 ;
nWeight[0][1][2] = 2 ;
nWeight[0][2][0] = -1 ;
nWeight[0][2][1] = 0 ;
nWeight[0][2][2] = 1 ;
nWeight[1][0][0] = -1 ;
nWeight[1][0][1] = -2 ;
nWeight[1][0][2] = -1 ;
nWeight[1][1][0] = 0 ;
nWeight[1][1][1] = 0 ;
nWeight[1][1][2] = 0 ;
nWeight[1][2][0] = 1 ;
nWeight[1][2][1] = 2 ;
nWeight[1][2][2] = 1 ;//負號上下??? 已改成8個方向模板的值
nWeight[2][0][0] = 0 ;
nWeight[2][0][1] = -1 ;
nWeight[2][0][2] = -2 ;
nWeight[2][1][0] = 1 ;
nWeight[2][1][1] = 0 ;
nWeight[2][1][2] = -1 ;
nWeight[2][2][0] = 2 ;
nWeight[2][2][1] = 1 ;
nWeight[2][2][2] = 0 ;
nWeight[3][0][0] = 1 ;
nWeight[3][0][1] = 0 ;
nWeight[3][0][2] = -1 ;
nWeight[3][1][0] = 2 ;
nWeight[3][1][1] = 0 ;
nWeight[3][1][2] = -2 ;
nWeight[3][2][0] = 1 ;
nWeight[3][2][1] = 0 ;
nWeight[3][2][2] = -1 ;
nWeight[4][0][0] = 2 ;
nWeight[4][0][1] = 1 ;
nWeight[4][0][2] = 0 ;
nWeight[4][1][0] = 1 ;
nWeight[4][1][1] = 0 ;
nWeight[4][1][2] = -1 ;
nWeight[4][2][0] = 0 ;
nWeight[4][2][1] = -1 ;
nWeight[4][2][2] = -2 ;
nWeight[5][0][0] = 1 ;
nWeight[5][0][1] = 2 ;
nWeight[5][0][2] = 1 ;
nWeight[5][1][0] = 0 ;
nWeight[5][1][1] = 0 ;
nWeight[5][1][2] = 0 ;
nWeight[5][2][0] = -1 ;
nWeight[5][2][1] = -2 ;
nWeight[5][2][2] = -1 ;
nWeight[6][0][0] = 0 ;
nWeight[6][0][1] = 1 ;
nWeight[6][0][2] = 2 ;
nWeight[6][1][0] = -1 ;
nWeight[6][1][1] = 0 ;
nWeight[6][1][2] = 1 ;
nWeight[6][2][0] = -2 ;
nWeight[6][2][1] = -1 ;
nWeight[6][2][2] = 0 ;
nWeight[7][0][0] = -2 ;
nWeight[7][0][1] = -1 ;
nWeight[7][0][2] = 0 ;
nWeight[7][1][0] = -1 ;
nWeight[7][1][1] = 0 ;
nWeight[7][1][2] = 1 ;
nWeight[7][2][0] = 0 ;
nWeight[7][2][1] = -1 ;
nWeight[7][2][2] = 2 ;
//注意:每行的字節(jié)數(shù)必須是4的整數(shù)倍!!!先不考慮
Ns=height*width;
unsigned char* kk = new unsigned char[width * height]; //開始變換 initiion
for(i=0; i《height ; i++ )
//if(i==0)//tt change at 05.05.16
for(j=0 ; j《width ; j++ )
{
des[i*width + j]=0;//*(pdGrad+y*nWidth+x)
}
for(i=1; i《height-1 ; i++ )
{
for(j=1 ; j《width-1 ; j++ )
{
dGrad[0] = 0 ;
dGrad[1] = 0 ;
dGrad[2] = 0 ;
dGrad[3] = 0 ;
dGrad[4] = 0 ;
dGrad[5] = 0 ;
dGrad[6] = 0 ;
dGrad[7] = 0 ;
// sobel算子需要的各點象素值
// 模板第一行
nTmp[0][0] = src[(i-1)*width + j - 1 ];
nTmp[0][1] = src[(i-1)*width + j ] ;
nTmp[0][2] = src[(i-1)*width + j + 1 ] ;
// 模板第二行
nTmp[1][0] = src[i*width + j - 1 ] ;
nTmp[1][1] = src[i*width + j ] ;
nTmp[1][2] = src[i*width + j + 1 ] ;
// 模板第三行
nTmp[2][0] = src[(i+1)*width + j - 1 ] ;
nTmp[2][1] = src[(i+1)*width + j ] ;
nTmp[2][2] = src[(i+1)*width + j + 1 ] ;
// 計算梯度
for(yy=0; yy《3; yy++)
for(xx=0; xx《3; xx++)
{
dGrad[0] += nTmp[yy][xx] * nWeight[0][yy][xx] ;
dGrad[1] += nTmp[yy][xx] * nWeight[1][yy][xx] ;
dGrad[2] += nTmp[yy][xx] * nWeight[2][yy][xx] ;
dGrad[3] += nTmp[yy][xx] * nWeight[3][yy][xx] ;
dGrad[4] += nTmp[yy][xx] * nWeight[4][yy][xx] ;
dGrad[5] += nTmp[yy][xx] * nWeight[5][yy][xx] ;
dGrad[6] += nTmp[yy][xx] * nWeight[6][yy][xx] ;
dGrad[7] += nTmp[yy][xx] * nWeight[7][yy][xx] ;
}
for (xx=1;xx《8;xx++)
{
if (dGrad[xx]》dGrad[0])
dGrad[0]=dGrad[xx];
}
des[i*width + j]=dGrad[0];// 梯度值寫入src[i]
}
}
//設定閾值
int th[5120],newth[5120],shuN,newN,flagyuzhi;//winframe=32,ii,jj,initpos;
double thk,kmin,mvalue[8];
shuN=0;
thk=0.5;
for (i=0;i《Ns;i++)//每層的每個點
{
if ((i》=width) && (i《(Ns-width)))//若是非邊界點,則……
{
if ((i%width!=0) && ((i+1)%width!=0))
{
//每點做變換,首先求kirs(c)h算子
mvalue[0]=fabs(double(des[i+1]+des[i+width+1]+des[i+width]+
des[i+width-1]+des[i-1]-des[i-width-1]-
des[i-width]-des[i-width+1]));
mvalue[1]=fabs(double(des[i+width+1]+des[i+width]+
des[i+width-1]+des[i-1]+des[i-width-1]-
des[i-width]-des[i-width+1]-des[i+1]));
mvalue[2]=fabs(double(des[i+width]+des[i+width-1]+des[i-1]+
des[i-width-1]+des[i-width]-
des[i-width+1]-des[i+1]-des[i+width+1]));
mvalue[3]=fabs(double(des[i+width-1]+des[i-1]+
des[i-width-1]+des[i-width]+
des[i-width+1]-des[i+1]-des[i+width+1]-
des[i+width]));
mvalue[4]=fabs(double(des[i-1]+des[i-width-1]+
des[i-width]+des[i-width+1]+des[i+1]-
des[i+width+1]-des[i+width]-
des[i+width-1]));
mvalue[5]=fabs(double(des[i-width-1]+des[i-width]+
des[i-width+1]+des[i+1]+des[i+width+1]-
des[i+width]-des[i+width-1]-des[i-1]));
mvalue[6]=fabs(double(des[i-width]+des[i-width+1]+des[i+1]+
des[i+width+1]+des[i+width]-
des[i+width-1]-des[i-1]-des[i-width-1]));
mvalue[7]=fabs(double(des[i-width+1]+des[i+1]+des[i+width+1]+
des[i+width]+des[i+width-1]-
des[i-1]-des[i-width-1]-des[i-width]));
for (j=1;j《8;j++) //比較得出算子,mvalue[0]為最大
{
if (mvalue[0]《mvalue[j])
mvalue[0]=mvalue[j];
}
kk[i]=max(1,mvalue[0]/15);
if (shuN==0)
kmin=kk[i];
if (kk[i]》thk)
{
th[shuN]=i;
kmin=min(kmin,kk[i]);
shuN++;
if (shuN》=5*height)//若大于5*H個點,則重新確定
{
//AfxMessageBox(“l(fā)ll”);
thk=kmin;
newN=0;
for (j=0;j《shuN;j++)
{
if (kk[th[j]]》thk)
{
if (newN==0)
kmin=kk[th[j]];
newth[newN]=th[j];
kmin=min(kmin,kk[th[j]]);
newN++;
}
//else des[th[j]]=0;
}
for (j=0;j《5120;j++)
{
th[j]=newth[j];
}
shuN=newN;
}//重新確定完
}
//非邊界的每點變換結束
}
}
}//一層結束
for (i=0;i《Ns;i++)//每層的每個點
{
if (des[i]《thk)
des[i]=0;
}
thresh (des, width,height);
//菜單函數(shù)結束
}
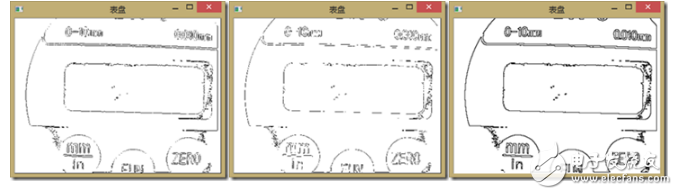
下面三圖分別為sobel、Roberts、kerish邊緣檢測的結果:
 電子發(fā)燒友App
電子發(fā)燒友App



































評論