邊緣檢測(cè)和圖像分割的聯(lián)系:
邊緣檢測(cè)是通過(guò)圖像的梯度變化將圖像中梯度變化明顯的地方檢測(cè)出來(lái),針對(duì)的是邊緣信息。圖像分割是將目標(biāo)分割出來(lái),針對(duì)的是目標(biāo)對(duì)象,邊緣檢測(cè)是空間域圖像分割的一種方法,屬于包含關(guān)系
邊緣檢測(cè)后的圖像是二值圖像,對(duì)二值圖像可以運(yùn)用形態(tài)學(xué)操作來(lái)分割目標(biāo),所以邊緣檢測(cè)是圖像分割的一個(gè)前提。但分割不一定非要用邊緣檢測(cè)。
圖像分割:
概念:
圖像分割是將圖像劃分成若干個(gè)互不相交的小區(qū)域的過(guò)程,所謂小區(qū)域是某種意義下具有共同屬性的像素的連通集合。
從集合的觀點(diǎn)看:它應(yīng)該是具有如下性質(zhì)的一種點(diǎn)集,集合R代表整個(gè)區(qū)域,對(duì)R的分割可看作將R分成N個(gè)滿(mǎn)足以下五個(gè)條件的非空子集R1,R2,…,RN:
目的:
無(wú)論是圖像處理、分析、理解與識(shí)別,其基礎(chǔ)工作一般都建立在圖像分割的基礎(chǔ)上;
將圖像中有意義的特征或者應(yīng)用所需要的特征信息提取出來(lái);
圖像分割的最終結(jié)果是將圖像分解成一些具有某種特征的單元,稱(chēng)為圖像的基元;
相對(duì)于整幅圖像來(lái)說(shuō),這種圖像基元更容易被快速處理。
圖像分割原理
圖像分割的研究多年來(lái)一直受到人們的高度重視,至今提出了各種類(lèi)型的分割算法。Pal把圖像分割算法分成了6類(lèi):閾值分割,像素分割、深度圖像分割、彩色圖像分割,邊緣檢測(cè)和基于模糊集的方法。但是,該方法中,各個(gè)類(lèi)別的內(nèi)容是有重疊的。為了涵蓋不斷涌現(xiàn)的新方法,有的研究者將圖像分割算法分為以下六類(lèi):并行邊界分割技術(shù)、串行邊界分割技術(shù)、并行區(qū)域分割技術(shù)、串行區(qū)域分割技術(shù)、結(jié)合特定理論工具的分割技術(shù)和特殊圖像分割技術(shù)。
圖像分割的特征:
分割出來(lái)的各區(qū)域?qū)δ撤N性質(zhì)例如灰度,紋理而言具有相似性,區(qū)域內(nèi)部是連通的的且沒(méi)有過(guò)多小孔。
區(qū)域邊界是明確的
相鄰區(qū)域?qū)Ψ指钏罁?jù)的性質(zhì)有明顯的差異
圖像分割的方法:
一、基于像素灰度值的分割方法:閾值(門(mén)限)方法
二、基于區(qū)域的分割方法:通過(guò)直接確定區(qū)域間的邊界來(lái)實(shí)現(xiàn)分割的邊界方法;
三、基于邊緣的分割技術(shù):首先檢測(cè)邊緣像素, 再將邊緣像素連接起來(lái)構(gòu)成邊界形成分割。
圖像分割包含的內(nèi)容:
邊緣檢測(cè)
邊緣跟蹤 :
從圖像中一個(gè)邊緣點(diǎn)出發(fā),然后根據(jù)某種判別準(zhǔn)則搜索下一個(gè)邊緣點(diǎn)以此跟蹤出目標(biāo)邊界。
閾值分割 :
原始圖像——f(x,y)
灰度閾值——T
閾值運(yùn)算得二值圖像——g(x,y)
區(qū)域分割:
閾值分割法由于沒(méi)有或很少考慮空間關(guān)系,使多閾值選擇受到限制
于區(qū)域的分割方法可以彌補(bǔ)這點(diǎn)不足,它利用的是圖像的空間性質(zhì),該方法認(rèn)為分割出來(lái)的屬于同一區(qū)域的像素應(yīng)具有相似的性質(zhì),其概念是相當(dāng)直觀的。
傳統(tǒng)的區(qū)域分割算法有區(qū)域增長(zhǎng)法和區(qū)域分裂合并法。該類(lèi)方法在沒(méi)有先驗(yàn)知識(shí)可以利用時(shí),對(duì)含有復(fù)雜場(chǎng)景或自然景物等先驗(yàn)知識(shí)不足的圖像進(jìn)行分割, 也可以取得較好的性能。但是,空間和時(shí)間開(kāi)銷(xiāo)都比較大。
區(qū)域生長(zhǎng)法主要考慮象素及其空間鄰域象素之間的關(guān)系
開(kāi)始時(shí)確定一個(gè)或多個(gè)象素點(diǎn)作為種子,然后按某種相似性準(zhǔn)則增長(zhǎng)區(qū)域,逐步生成具有某種均勻性的空間區(qū)域,將相鄰的具有相似性質(zhì)的象素或區(qū)域歸并從而逐步增長(zhǎng)區(qū)域,直至沒(méi)有可以歸并的點(diǎn)或其它小區(qū)域?yàn)橹埂?/p>
區(qū)域內(nèi)象素的相似性度量可以包括平均灰度值、紋理、顏色等信息。
區(qū)域生長(zhǎng):
主要考慮像素及其空間鄰域像素之間的關(guān)系
開(kāi)始時(shí)確定一個(gè)或多個(gè)像素點(diǎn)作為種子,然后按某種相似性準(zhǔn)則增長(zhǎng)區(qū)域,逐步生成具有某種均勻性的空間區(qū)域,將相鄰的具有相似性質(zhì)的像素或區(qū)域歸并從而逐步增長(zhǎng)區(qū)域,直至沒(méi)有可以歸并的點(diǎn)或其它小區(qū)域?yàn)橹埂?/p>
區(qū)域內(nèi)像素的相似性度量可以包括平均灰度值、紋理、顏色等信息。
主要步驟:
選擇合適的種子點(diǎn)
確定相似性準(zhǔn)則(生長(zhǎng)準(zhǔn)則)
確定生長(zhǎng)停止條件
區(qū)域分裂:
條件:如果區(qū)域的某些特性不滿(mǎn)足一致性準(zhǔn)則
開(kāi)始:從圖像的最大區(qū)域開(kāi)始,一般情況下,是從整幅圖像開(kāi)始
注意:
確定分裂準(zhǔn)則(一致性準(zhǔn)則)
確定分裂方法,即如何分裂區(qū)域,使得分裂后的子區(qū)域的特性盡可能都滿(mǎn)足一致性準(zhǔn)則值
邊緣檢測(cè):
在視覺(jué)計(jì)算理論框架中,抽取二維圖像上的邊緣、角點(diǎn)、紋理等基本特征,是整個(gè)系統(tǒng)框架中的第一步。這些特征所組成的圖稱(chēng)為基元圖。
在不同“尺度”意義下的邊緣點(diǎn),在一定條件下包含了原圖像的全部信息。
定義:
?目前,具有對(duì)邊緣的描述性定義,即兩個(gè)具有不同灰度的均勻圖像區(qū)域的邊界,即邊界反映局部的灰度變化。
?局部邊緣是圖像中局部灰度級(jí)以簡(jiǎn)單(即單調(diào))的方式作極快變換的小區(qū)域。這種局部變化可用一定窗口運(yùn)算的邊緣檢測(cè)算子來(lái)檢測(cè)。
邊緣的描述:
1) 邊緣法線(xiàn)方向——在某點(diǎn)灰度變化最劇烈的方向,與邊緣方向垂直;
2) 邊緣方向——與邊緣法線(xiàn)方向垂直,是目標(biāo)邊界的切線(xiàn)方向;
3) 邊緣強(qiáng)度——沿邊緣法線(xiàn)方向圖像局部的變化強(qiáng)度的量度。
邊緣檢測(cè)的基本思想是通過(guò)檢測(cè)每個(gè)像素和其鄰域的狀態(tài),以決定該像素是否位于一個(gè)物體的邊界上。如果一個(gè)像素位于一個(gè)物體的邊界上,則其鄰域像素的灰度值的變化就比較大。假如可以應(yīng)用某種算法檢測(cè)出這種變化并進(jìn)行量化表示,那么就可以確定物體的邊界。
邊緣檢測(cè)算法有如下四個(gè)步驟:
濾波:邊緣檢測(cè)算法主要是基于圖像強(qiáng)度的一階和二階導(dǎo)數(shù),但導(dǎo)數(shù)的計(jì)算對(duì)噪聲很敏感,因此必須使用濾波器來(lái)改善與噪聲有關(guān)的邊緣檢測(cè)器的性能.需要指出,大多數(shù)濾波器在降低噪聲的同時(shí)也導(dǎo)致了邊緣強(qiáng)度的損失,因此,增強(qiáng)邊緣和降低噪聲之間需要折衷.
增強(qiáng):增強(qiáng)邊緣的基礎(chǔ)是確定圖像各點(diǎn)鄰域強(qiáng)度的變化值.增強(qiáng)算法可以將鄰域(或局部)強(qiáng)度值有顯著變化的點(diǎn)突顯出來(lái).邊緣增強(qiáng)一般是通過(guò)計(jì)算梯度幅值來(lái)完成的.
檢測(cè):在圖像中有許多點(diǎn)的梯度幅值比較大,而這些點(diǎn)在特定的應(yīng)用領(lǐng)域中并不都是邊緣,所以應(yīng)該用某種方法來(lái)確定哪些點(diǎn)是邊緣點(diǎn).最簡(jiǎn)單的邊緣檢測(cè)判據(jù)是梯度幅值閾值判據(jù).
定位:如果某一應(yīng)用場(chǎng)合要求確定邊緣位置,則邊緣的位置可在子像素分辨率上來(lái)估計(jì),邊緣的方位也可以被估計(jì)出來(lái).
在邊緣檢測(cè)算法中,前三個(gè)步驟用得十分普遍。這是因?yàn)榇蠖鄶?shù)場(chǎng)合下,僅僅需要邊緣檢測(cè)器指出邊緣出現(xiàn)在圖像某一像素點(diǎn)的附近,而沒(méi)有必要指出邊緣的精確位置或方向.邊緣檢測(cè)誤差通常是指邊緣誤分類(lèi)誤差,即把假邊緣判別成邊緣而保留,而把真邊緣判別成假邊緣而去掉.邊緣估計(jì)誤差是用概率統(tǒng)計(jì)模型來(lái)描述邊緣的位置和方向誤差的.我們將邊緣檢測(cè)誤差和邊緣估計(jì)誤差區(qū)分開(kāi),是因?yàn)樗鼈兊挠?jì)算方法完全不同,其誤差模型也完全不同.
邊緣檢測(cè)的三個(gè)共性準(zhǔn)則:
?好的檢測(cè)結(jié)果,或者說(shuō)對(duì)邊緣的誤測(cè)率盡可能低,就是在圖像邊緣出現(xiàn)的地方檢測(cè)結(jié)果中不應(yīng)該沒(méi)有;另一方面不要出現(xiàn)虛假的邊緣;
?對(duì)邊緣的定位要準(zhǔn)確,也就是我們標(biāo)記出的邊緣位置要和圖像上真正邊緣的中心位置充分接近;
?對(duì)同一邊緣要有盡可能低的響應(yīng)次數(shù),也就是檢測(cè)響應(yīng)最好是單像素的。
幾種常用的邊緣檢測(cè)算子主要有Roberts邊緣檢測(cè)算子,Sobel算子、Prewitt算子、Krisch邊緣算子,高斯-拉普拉斯算子。
圖像特征:
?圖像特征是指圖像中可用作標(biāo)志的屬性,它可以分為統(tǒng)計(jì)特征和視覺(jué)特征兩類(lèi)。
?圖像的統(tǒng)計(jì)特征是指一些人為定義的特征,通過(guò)變換才能得到,如圖像的直方圖、矩、頻譜等;
?圖像的視覺(jué)特征是指人的視覺(jué)可直接感受到的自然特征,如區(qū)域的亮度、紋理或輪廓等
輪廓提取:
二值圖像輪廓提取的算法非常簡(jiǎn)單, 就是掏空內(nèi)部點(diǎn): 如果原圖像中有一點(diǎn)為黑,且它的8個(gè)鄰點(diǎn)都是黑色時(shí),說(shuō)明該點(diǎn)是內(nèi)部點(diǎn), 將該點(diǎn)刪除(置為白色像素值255)。對(duì)圖像中所有像素點(diǎn)執(zhí)行該操作便可完成圖像輪廓的提取。
模板匹配:
模板匹配是指用一個(gè)較小的圖像,即模板與源圖像進(jìn)行比較, 以確定在源圖像中是否存在與該模板相同或相似的區(qū)域, 若該區(qū)域存在, 還可確定其位置并提取該區(qū)域。
形狀匹配:
形狀也是描述圖像內(nèi)容的一個(gè)重要特征, 利用形狀進(jìn)行匹配需要考慮三個(gè)問(wèn)題。首先,形狀常與目標(biāo)聯(lián)系在一起,所以相對(duì)于顏色, 形狀特征可以看作是更高層次的圖像特征。要獲得有關(guān)目標(biāo)的形狀參數(shù),常常要先對(duì)圖像進(jìn)行分割, 所以形狀特征會(huì)受圖像分割效果的影響。其次,目標(biāo)形狀的描述是一個(gè)非常復(fù)雜的問(wèn)題,至今還沒(méi)有找到能與人的感覺(jué)相一致的圖像形狀的確切數(shù)學(xué)定義。最后,從不同視角獲取的圖像中目標(biāo)形狀可能會(huì)有很大差別,為準(zhǔn)確進(jìn)行形狀匹配,需要解決平移、 尺度、 旋轉(zhuǎn)變換不變性的問(wèn)題。
標(biāo)的形狀常常可以用目標(biāo)的輪廓來(lái)表示,而輪廓是由一系列邊界點(diǎn)所組成的。一般認(rèn)為,在較大尺度下常常能較可靠地消除誤檢并檢測(cè)到真正的邊界點(diǎn), 但在大尺度下對(duì)邊界的定位不易準(zhǔn)確。相反,在較小尺度下對(duì)真正邊界點(diǎn)的定位常比較準(zhǔn)確,但在小尺度下誤檢的比例會(huì)增加。所以,可考慮先在較大尺度下檢測(cè)出真正的邊界點(diǎn),再在較小尺度下對(duì)真正邊界點(diǎn)進(jìn)行較精確的定位。小波變換和分析作為一種多尺度、 多通道分析工具,比較適合對(duì)圖像進(jìn)行多尺度的邊界檢測(cè)。
圖像分割的實(shí)現(xiàn)
我用了Roberts算子、Sobel算子和Kirsh算子邊緣檢測(cè)的方法但都由于亮度不均等因素對(duì)圖像分割的效果不太好:
Sobel:
void sobel (unsignedchar* des, constunsignedchar* src, int width, int height)
{
for (int y=0; y《height; y++)
for (int x=0; x《width; x++)
des[y * width + x]=255;
/* Now compute the convolution, scaling */
for (int y=1; y《height-1; y++)
for (int x=1; x《width-1; x++)
{
double n = (src[(y+1)*width+x-1]+2*src[(y+1)*width+x]+src[(y+1)*width+x+1]) -
(src[(y-1)*width+x-1]+2*src[(y-1)*width+x]+src[(y-1)*width+x+1]);
double m = (src[(y-1)*width+x+1]+2*src[y*width+x+1]+src[(y+1)*width+x+1])-
(src[(y-1)*width+x-1]+2*src[y*width+x-1]+src[(y+1)*width+x-1]);
double k = (int)( sqrt( (double)(n*n + m*m) )/4.0 );
des[y * width + x] = k;
}
thresh (des, width,height);
}
Roberts算子:
void roberts(unsignedchar* des, constunsignedchar* src, int width, int height)
{
for (int y=0; y《height; y++)
for (int x=0; x《width; x++)
des[y * width + x]=255;
/* Now compute the convolution, scaling */
for (int y=1; y《height-1; y++)
for (int x=1; x《width-1; x++)
{
double n = src[y*width+x] - src[(y+1)*width+x+1];
double m = src[(y+1)*width+x] - src[y*width+x+1];
double k = abs(m)+abs(n);
des[y * width + x] = k;
}
thresh (des, width,height);
}
Kirsch算子:
void kirsch(unsigned char* des, const unsigned char* src, int width, int height)
{
// TODO: Add your command handler code here
//顯示數(shù)值
long int i,j,Ns;
static int nWeight[8][3][3];//對(duì)一個(gè)靜態(tài)整型數(shù)組賦初值,模板
double dGrad[8];
int nTmp[3][3],xx,yy;//每像素點(diǎn)的鄰域值
nWeight[0][0][0] = -1 ;
nWeight[0][0][1] = 0 ;
nWeight[0][0][2] = 1 ;
nWeight[0][1][0] = -2 ;
nWeight[0][1][1] = 0 ;
nWeight[0][1][2] = 2 ;
nWeight[0][2][0] = -1 ;
nWeight[0][2][1] = 0 ;
nWeight[0][2][2] = 1 ;
nWeight[1][0][0] = -1 ;
nWeight[1][0][1] = -2 ;
nWeight[1][0][2] = -1 ;
nWeight[1][1][0] = 0 ;
nWeight[1][1][1] = 0 ;
nWeight[1][1][2] = 0 ;
nWeight[1][2][0] = 1 ;
nWeight[1][2][1] = 2 ;
nWeight[1][2][2] = 1 ;//負(fù)號(hào)上下??? 已改成8個(gè)方向模板的值
nWeight[2][0][0] = 0 ;
nWeight[2][0][1] = -1 ;
nWeight[2][0][2] = -2 ;
nWeight[2][1][0] = 1 ;
nWeight[2][1][1] = 0 ;
nWeight[2][1][2] = -1 ;
nWeight[2][2][0] = 2 ;
nWeight[2][2][1] = 1 ;
nWeight[2][2][2] = 0 ;
nWeight[3][0][0] = 1 ;
nWeight[3][0][1] = 0 ;
nWeight[3][0][2] = -1 ;
nWeight[3][1][0] = 2 ;
nWeight[3][1][1] = 0 ;
nWeight[3][1][2] = -2 ;
nWeight[3][2][0] = 1 ;
nWeight[3][2][1] = 0 ;
nWeight[3][2][2] = -1 ;
nWeight[4][0][0] = 2 ;
nWeight[4][0][1] = 1 ;
nWeight[4][0][2] = 0 ;
nWeight[4][1][0] = 1 ;
nWeight[4][1][1] = 0 ;
nWeight[4][1][2] = -1 ;
nWeight[4][2][0] = 0 ;
nWeight[4][2][1] = -1 ;
nWeight[4][2][2] = -2 ;
nWeight[5][0][0] = 1 ;
nWeight[5][0][1] = 2 ;
nWeight[5][0][2] = 1 ;
nWeight[5][1][0] = 0 ;
nWeight[5][1][1] = 0 ;
nWeight[5][1][2] = 0 ;
nWeight[5][2][0] = -1 ;
nWeight[5][2][1] = -2 ;
nWeight[5][2][2] = -1 ;
nWeight[6][0][0] = 0 ;
nWeight[6][0][1] = 1 ;
nWeight[6][0][2] = 2 ;
nWeight[6][1][0] = -1 ;
nWeight[6][1][1] = 0 ;
nWeight[6][1][2] = 1 ;
nWeight[6][2][0] = -2 ;
nWeight[6][2][1] = -1 ;
nWeight[6][2][2] = 0 ;
nWeight[7][0][0] = -2 ;
nWeight[7][0][1] = -1 ;
nWeight[7][0][2] = 0 ;
nWeight[7][1][0] = -1 ;
nWeight[7][1][1] = 0 ;
nWeight[7][1][2] = 1 ;
nWeight[7][2][0] = 0 ;
nWeight[7][2][1] = -1 ;
nWeight[7][2][2] = 2 ;
//注意:每行的字節(jié)數(shù)必須是4的整數(shù)倍!!!先不考慮
Ns=height*width;
unsigned char* kk = new unsigned char[width * height]; //開(kāi)始變換 initiion
for(i=0; i《height ; i++ )
//if(i==0)//tt change at 05.05.16
for(j=0 ; j《width ; j++ )
{
des[i*width + j]=0;//*(pdGrad+y*nWidth+x)
}
for(i=1; i《height-1 ; i++ )
{
for(j=1 ; j《width-1 ; j++ )
{
dGrad[0] = 0 ;
dGrad[1] = 0 ;
dGrad[2] = 0 ;
dGrad[3] = 0 ;
dGrad[4] = 0 ;
dGrad[5] = 0 ;
dGrad[6] = 0 ;
dGrad[7] = 0 ;
// sobel算子需要的各點(diǎn)象素值
// 模板第一行
nTmp[0][0] = src[(i-1)*width + j - 1 ];
nTmp[0][1] = src[(i-1)*width + j ] ;
nTmp[0][2] = src[(i-1)*width + j + 1 ] ;
// 模板第二行
nTmp[1][0] = src[i*width + j - 1 ] ;
nTmp[1][1] = src[i*width + j ] ;
nTmp[1][2] = src[i*width + j + 1 ] ;
// 模板第三行
nTmp[2][0] = src[(i+1)*width + j - 1 ] ;
nTmp[2][1] = src[(i+1)*width + j ] ;
nTmp[2][2] = src[(i+1)*width + j + 1 ] ;
// 計(jì)算梯度
for(yy=0; yy《3; yy++)
for(xx=0; xx《3; xx++)
{
dGrad[0] += nTmp[yy][xx] * nWeight[0][yy][xx] ;
dGrad[1] += nTmp[yy][xx] * nWeight[1][yy][xx] ;
dGrad[2] += nTmp[yy][xx] * nWeight[2][yy][xx] ;
dGrad[3] += nTmp[yy][xx] * nWeight[3][yy][xx] ;
dGrad[4] += nTmp[yy][xx] * nWeight[4][yy][xx] ;
dGrad[5] += nTmp[yy][xx] * nWeight[5][yy][xx] ;
dGrad[6] += nTmp[yy][xx] * nWeight[6][yy][xx] ;
dGrad[7] += nTmp[yy][xx] * nWeight[7][yy][xx] ;
}
for (xx=1;xx《8;xx++)
{
if (dGrad[xx]》dGrad[0])
dGrad[0]=dGrad[xx];
}
des[i*width + j]=dGrad[0];// 梯度值寫(xiě)入src[i]
}
}
//設(shè)定閾值
int th[5120],newth[5120],shuN,newN,flagyuzhi;//winframe=32,ii,jj,initpos;
double thk,kmin,mvalue[8];
shuN=0;
thk=0.5;
for (i=0;i《Ns;i++)//每層的每個(gè)點(diǎn)
{
if ((i》=width) && (i《(Ns-width)))//若是非邊界點(diǎn),則……
{
if ((i%width!=0) && ((i+1)%width!=0))
{
//每點(diǎn)做變換,首先求kirs(c)h算子
mvalue[0]=fabs(double(des[i+1]+des[i+width+1]+des[i+width]+
des[i+width-1]+des[i-1]-des[i-width-1]-
des[i-width]-des[i-width+1]));
mvalue[1]=fabs(double(des[i+width+1]+des[i+width]+
des[i+width-1]+des[i-1]+des[i-width-1]-
des[i-width]-des[i-width+1]-des[i+1]));
mvalue[2]=fabs(double(des[i+width]+des[i+width-1]+des[i-1]+
des[i-width-1]+des[i-width]-
des[i-width+1]-des[i+1]-des[i+width+1]));
mvalue[3]=fabs(double(des[i+width-1]+des[i-1]+
des[i-width-1]+des[i-width]+
des[i-width+1]-des[i+1]-des[i+width+1]-
des[i+width]));
mvalue[4]=fabs(double(des[i-1]+des[i-width-1]+
des[i-width]+des[i-width+1]+des[i+1]-
des[i+width+1]-des[i+width]-
des[i+width-1]));
mvalue[5]=fabs(double(des[i-width-1]+des[i-width]+
des[i-width+1]+des[i+1]+des[i+width+1]-
des[i+width]-des[i+width-1]-des[i-1]));
mvalue[6]=fabs(double(des[i-width]+des[i-width+1]+des[i+1]+
des[i+width+1]+des[i+width]-
des[i+width-1]-des[i-1]-des[i-width-1]));
mvalue[7]=fabs(double(des[i-width+1]+des[i+1]+des[i+width+1]+
des[i+width]+des[i+width-1]-
des[i-1]-des[i-width-1]-des[i-width]));
for (j=1;j《8;j++) //比較得出算子,mvalue[0]為最大
{
if (mvalue[0]《mvalue[j])
mvalue[0]=mvalue[j];
}
kk[i]=max(1,mvalue[0]/15);
if (shuN==0)
kmin=kk[i];
if (kk[i]》thk)
{
th[shuN]=i;
kmin=min(kmin,kk[i]);
shuN++;
if (shuN》=5*height)//若大于5*H個(gè)點(diǎn),則重新確定
{
//AfxMessageBox(“l(fā)ll”);
thk=kmin;
newN=0;
for (j=0;j《shuN;j++)
{
if (kk[th[j]]》thk)
{
if (newN==0)
kmin=kk[th[j]];
newth[newN]=th[j];
kmin=min(kmin,kk[th[j]]);
newN++;
}
//else des[th[j]]=0;
}
for (j=0;j《5120;j++)
{
th[j]=newth[j];
}
shuN=newN;
}//重新確定完
}
//非邊界的每點(diǎn)變換結(jié)束
}
}
}//一層結(jié)束
for (i=0;i《Ns;i++)//每層的每個(gè)點(diǎn)
{
if (des[i]《thk)
des[i]=0;
}
thresh (des, width,height);
//菜單函數(shù)結(jié)束
}
下面三圖分別為sobel、Roberts、kerish邊緣檢測(cè)的結(jié)果:
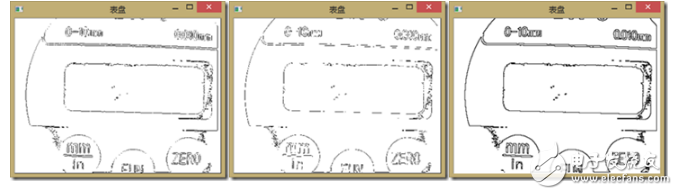
之后打算用霍夫變換檢測(cè)直線(xiàn)找矩形框,但是由于光照形成的噪點(diǎn)效果并不是很好,因此最后用自適應(yīng)直方圖均衡去除光照影響加自適應(yīng)中值濾波再用投影法實(shí)現(xiàn)矩形框和數(shù)字的檢測(cè)。具體如下:
int main()
{
IplImage* src = cvLoadImage(“dm5.bmp”);
IplImage* gray = cvCreateImage(cvGetSize(src), src-》depth, 1);
cvCvtColor(src,gray,CV_BGR2GRAY); //灰度化
int width = src-》width;
int height = src-》height;
IplImage* dst = cvCreateImage(cvGetSize(src), src-》depth, gray-》nChannels);
IplImage* scr = cvCreateImage(cvGetSize(gray), gray-》depth, gray-》nChannels);
cvSmooth(gray, gray, CV_MEDIAN, 3, 0, 0, 0); //中值濾波,消除小的噪聲;
cvSmooth(gray, gray, CV_GAUSSIAN, 9, gray-》nChannels);//高斯濾波
cvCvtColor(src,scr,CV_BGR2GRAY);
cvThreshold( gray, gray, 190, 255, CV_THRESH_BINARY);//二值化
int nChannels =gray-》nChannels;
cvNamedWindow(“origin”,0);
cvResizeWindow(“origin”,int(width/2),int(height/2));
cvShowImage(“origin”, src);
unsigned char* img = new unsigned char[width * height ];
unsigned char* des = new unsigned char[width * height ];
unsigned char* gra = new unsigned char[width * height];
unsigned char* grt = new unsigned char[width * height];
img_data(gray, gra,width,height, nChannels);
img_data(scr, img,width,height,nChannels);
AHE(des, img, width, height,nChannels,10);//自適應(yīng)直方圖均衡
Projection( grt,gra,width,height); //投影檢測(cè)表盤(pán)區(qū)域
img_extract(des,grt,width,height,1); //表盤(pán)區(qū)域還原
//kirsch(des,gra, width,height);
data_img( scr, des, width, height, nChannels);
cvNamedWindow(“表盤(pán)”,0);
cvResizeWindow(“表盤(pán)”,int(width/2),int(height/2));
cvShowImage(“表盤(pán)”, scr);
cvThreshold(scr, scr, 100, 255, CV_THRESH_BINARY); //表盤(pán)區(qū)域二值化以查找數(shù)字
img_data(scr, img,width,height,nChannels);
Adaptivemedianfilter(des, img, width, height, nChannels); //自適應(yīng)中值濾波去噪
ImageDilation( img, des, width, height,nChannels,1);
ImageErosion( des,img,width, height,nChannels,1); //經(jīng)過(guò)一次膨脹腐蝕去噪
location(img, des, width, height); //找出數(shù)字所在區(qū)域
data_img( scr, img, width, height, nChannels);
cvNamedWindow(“數(shù)字”,0);
cvResizeWindow(“數(shù)字”,int(width/2),int(height/2));
cvSaveImage(“123.bmp”,scr);
cvShowImage(“數(shù)字”, scr);
data_img( gray,des, width, height, nChannels);
cvNamedWindow(“erzhi”,0);
cvResizeWindow(“erzhi”,int(width/2),int(height/2));
cvShowImage(“erzhi”, gray);
cvWaitKey(0);
}
/**************************************************************************
函數(shù)名:Projection
功 能:投影法找出矩形區(qū)域
輸 入:目標(biāo)圖像des, 原圖像 src,圖像寬width, 高h(yuǎn)eight
返回值:no
*************************************************************************/
void Projection(unsigned char* des, const unsigned char* src,int width, int height)
{
int* h_sum = new int[height];
int* w_sum = new int[width];
int up=0;
int below=height;
int left=0;
int right=width;
for(int y=0;y《height;y++)
{
for(int x=0;x《width;x++)
{
des[y*width+x]=255;
}
}
for(int y=0;y《height;y++)
{
h_sum[y]=0;
for(int x=0;x《width;x++)
{
//printf(“src %d”,src[y*width+x]);
h_sum[y]=h_sum[y]+src[y*width+x];
}
//printf(“%d行%d ”,y,h_sum[y]);
}
for(int y=height/2;y《height;y++)
{
if((h_sum[y]-h_sum[height/2])》255*60)
{
below=y;
break;
}
}
for(int y=height/2;y》0;y--)
{
if((h_sum[y]-h_sum[height/2])》255*60)
{
up=y;
break;
}
}
for(int x=0;x《width;x++)
{
w_sum[x]=0;
for(int y=up;y《below;y++)
{
w_sum[x]=w_sum[x]+src[y*width+x];
}
//printf(“%d列%d ”,x,w_sum[x]);
}
int max_r=0;
int max_l=0;
for(int x=width/2+100;x《width;x++)
{
if(w_sum[x]》max_r)
{
right=x;
max_r=w_sum[x];
}
}
for(int x=width/2-100;x》0;x--)
{
if(w_sum[x]》max_l)
{
left=x;
max_l=w_sum[x];
}
}
for(int y=up;y《below;y++)
{
for(int x=left;x《right;x++)
{
des[y*width+x]=0;
}
}
printf(“up%d below%d left%d right%d”,up, below,left, right);
}
void img_extract(unsigned char* des, const unsigned char* src,int width, int height, int nChannels)
{
for (int y=0;y《height;y++)
for(int x=0;x《width;x++)
if(src[y*width+x]!=0)
{
for(int n = 0; n 《 nChannels; n++)
{
des[y * width * nChannels + x * nChannels + n ] = 255;
}
}
}
/************************************************************************
函數(shù)名:location
功 能:投影法找出數(shù)字
輸 入:目標(biāo)圖像des, 原圖像 src,圖像寬width, 高h(yuǎn)eight
返回值:no
**********************************************************************/
void location(unsigned char* des, const unsigned char* src,int width, int height)
{
int* h_sum = new int[height];
int* w_sum = new int[width];
int up=0;
int below=height;
int left=0;
int right=width;
for(int y=0;y《height;y++)
{
for(int x=0;x《width;x++)
{
des[y*width+x]=255;
}
}
for(int y=0;y《height;y++)
{
h_sum[y]=0;
for(int x=0;x《width;x++)
{
//printf(“src %d”,src[y*width+x]);
h_sum[y]=h_sum[y]+src[y*width+x];
}
//printf(“%d行%d ”,y,h_sum[y]);
}
int h_mid=(h_sum[height/2]+h_sum[height/2-10]+h_sum[height/2-20]+h_sum[height/2-30]+h_sum[height/2-40]);
h_mid=h_mid/5;
for(int y=height/2;y《height;y++)
{
if((h_sum[y]-h_mid)》255*35)
{
below=y;
break;
}
}
for(int y=height/2;y》0;y--)
{
if((h_sum[y]-h_mid)》255*37)
{
up=y;
break;
}
}
for(int x=0;x《width;x++)
{
w_sum[x]=0;
for(int y=up;y《below;y++)
{
w_sum[x]=w_sum[x]+src[y*width+x];
}
//printf(“%d列%d ”,x,w_sum[x]);
}
int right_start=width-10;
for(int x=width-10;x》width/2;x--)
{
if(w_sum[x]!=(below-up)*255)
{
right_start=x;
break;
}
}
for(int x=right_start-45;x》width/2;x--)
{
if(w_sum[x]《255*(below-up-40))
{
right=x;
break;
}
}
int left_start=10;
for(int x=10;x《width;x++)
{
if(w_sum[x]!=(below-up)*255)
{
left_start=x;
break;
}
}
for(int x=left_start+100;x《width;x++)
{
if(w_sum[x]《255*(below-up-20))
{
left=x;
break;
}
}
for(int y=up;y《below;y++)
{
for(int x=left-5;x《right+5;x++)
{
des[y*width+x]=src[y*width+x];
}
}
printf(“up%d below%d left%d right%d left_start%d h_mid%d height/2%d width%d”,up, below,left, right,left_start,h_mid,height/2,width);
}
結(jié)果展示
 電子發(fā)燒友App
電子發(fā)燒友App















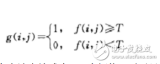




















評(píng)論