等效電阻

　　幾個連接起來的電阻所起的作用，可以用一個電阻來代替，這個電阻就是那些電阻的等效電阻。也就是說任何電回路中的電阻，不論有多少只，都可等效為一個電阻來代替。而不影響原回路兩端的電壓和回路中電流強度的變化。這個等效電阻，是由多個電阻經過等效串并聯公式，計算出等效電阻的大小值。也可以說，將這一等效電阻代替原有的幾個電阻后，對于整個電路的電壓和電流量不會產生任何的影響，所以這個電阻就叫做回路中的等效電阻。

　　就是用一個電阻代替串聯電路中幾個電阻，比如一個串聯電路中有2個電阻，可以用另一個電阻來代替它們。首先把這兩個電阻串聯起來，然后移動滑動變阻器，移動到適當的地方就可以，然后記錄下這時的電壓與電流，分別假設為U和I。然后就另外把電阻箱接入電路中，滑動變阻器不要移動，保持原樣，調整變阻器的阻值，使得電壓和電流為I和U。

在電路分析中，最基本的電路就是電阻電路。而分析電阻電路常常要將電路化簡，求其等效電阻。由于實際電路形式多種多樣，電阻之間聯接方式也不盡相同，因此等效電阻計算方法也有所不同。本文就幾種常見的電阻聯接方式，談談等效電阻的計算方法和技巧。

一、電阻的串聯

以3個電阻聯接為例，電路如圖1所示。

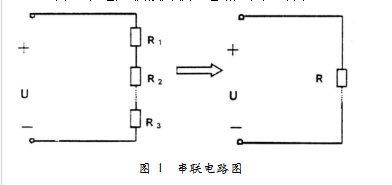
根據電阻串聯特點可推得，等效電阻等于各串聯電阻之和，即

由此可見：

（1）串聯電阻越多，等效電阻也越大;

（2）如果各電阻阻值相同，則等效電阻為R=nR1

二、電阻的并聯

電路如圖2所示。

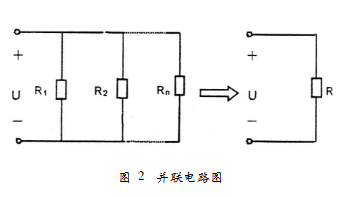
根據電阻并聯特點可推得，等效電阻的倒數等

于各并聯電阻倒數之和，即：

上述結論能否推廣使用呢？即如果一個電阻是另一個電阻的3倍、4倍，，n倍。

例如，128電阻分別與48、38、28、18電阻并聯（它們的倍數分別是3、4、6和12倍），等效電阻如何計算？

不難看出：當一電阻為另一電阻的n倍時，等效電阻的計算通式為

三、電阻的混聯

在實際電路中，單純的電阻串聯或并聯是不多見的，更常見的是既有串聯，又有并聯，即電阻的混聯電路。

對于混聯電路等效電阻計算，分別可從以下兩種情況考慮。

1.電阻之間聯接關系比較容易確定

求解方法是：先局部，后整體，即先確定局部電阻串聯、并聯關系，根據串、并聯等效電阻計算公式，分別求出局部等效電阻，然后逐步將電路化簡，最后求出總等效電阻。

例如圖3所示電路，從a、b兩端看進去，R1與R2并聯，R3與R4并聯，前者等效電阻與后者等效電阻串聯，R5的兩端處于同一點（b點）而被短接，計算時不須考慮，所以，等效電阻：

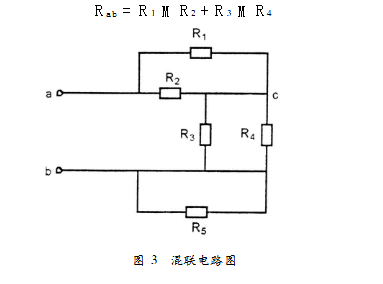
值得注意的是：等效電阻的計算與對應端點有關，也就是說不同的兩點看進去，等效電阻往往是不一樣的，因為對應點不同，電阻之間的聯接關系可能不同。

例如圖3，若從a、c兩點看進去，R1與R2并聯，R3與R4就不是并聯，而是串聯（但此時R3+R4被短接），這樣，等效電阻為：

Rac=R1MR2

同理，從b、c看進去，R1與R2串聯（被短接），R3與R4并聯，等效電阻：

Rbc=R3MR4

2.電阻之間聯接關系不太容易確定

例如圖4所示，各電阻的串、并聯關系不是很清晰，對初學者來說，直接求解比較困難。所以，可將原始電路進行改畫，使之成為電阻聯接關系比較明顯的電路，然后再進行計算。

具體方法步驟如下：

（1）找出電路各節點，并對其進行命名，如圖5所示。

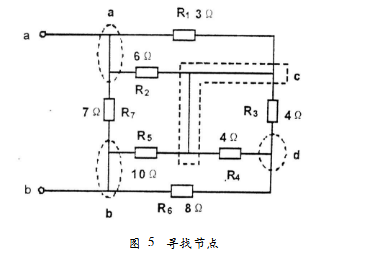
在找節點時需注意：

等電位點屬于同一點，故不能重復命名，如上圖的c點，它是由三個等電位點構成的，命名時必須將它們看成一點。

（2）將各節點畫在一條水平線上，如圖6所示。

布局各節點時需注意：為方便計算，最好將兩端點分別畫在兩頭，如圖6的a、b兩點。

（3）對號入座各電阻，畫出新電路。即將各電阻分別畫在對應節點之間，這樣，就構成了一個與原始電路實質相同，而形式比較簡單明了的新電路了，如圖7所示。最后再求等效電阻。

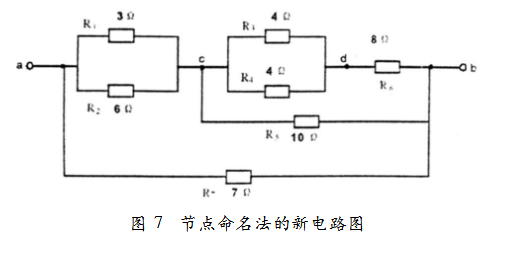
此方法可稱為節點命名法。它是分析電阻聯接關系比較復雜電路的一種實用的方法。

四、電阻的星形（Y）與三角形（v）聯接電路

求解這類電路等效電阻的基本思路，就是將電路作星形與三角等效互換，使之變成電阻串、并聯電路。

例如圖8所示電路。

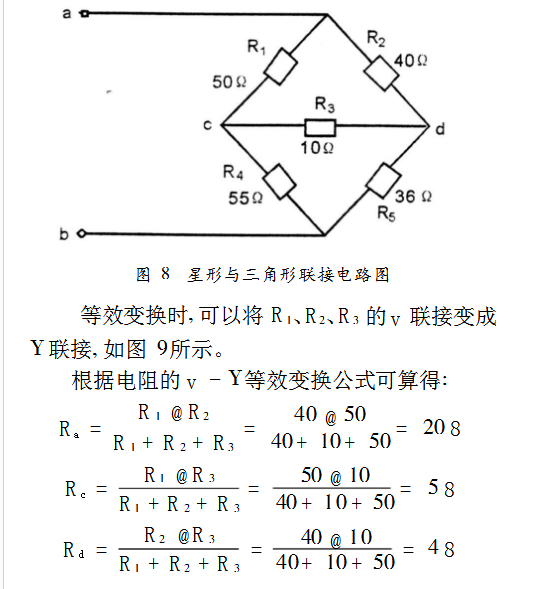
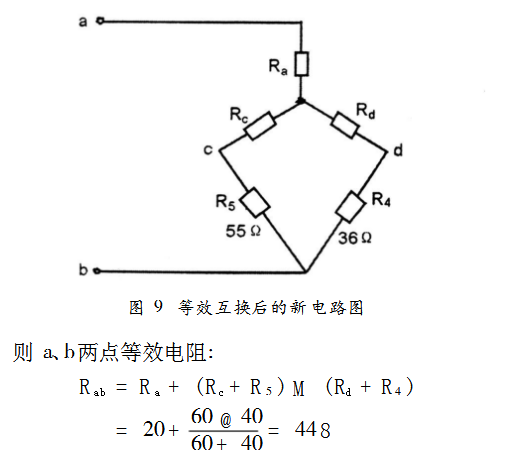
此題還可以將R3、R4、R5變成Y形，或者將R1、R3、R4變成v（也可將R2、R3、R5變成v）等方法化簡進行計算。