本文所測為P級精度的滾珠螺母GQ25×6,文獻[2]給出了其技術規范。現對其滾道圓度誤差、圓柱度誤差、跳動誤差及同軸度誤差等參數進行測量。

　　4.1　滾道圓度誤差測量

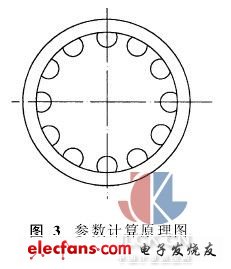
　　將內螺紋裝卡在分度頭上,標準測球放置在滾道內,在一個螺距范圍內采集N個圖像,使每兩次采集圖像之間螺母沿固定方向旋轉360°/N,計算度量測球中心點(X0,Y0)和螺母外圓柱面中心點(Xb,Yb)的亞像素坐標,以此計算形位誤差。由于內螺紋外圓柱面的加工精度較高,形狀誤差很小,故將其視為理想圓柱面,在N個圖像中,其中心的位置相對于圓周像素保持不變。以螺母外圓柱面為基準,將各圖像測球中心坐標通過外圓柱面中心坐標和標定系數統一在一個坐標中,如圖3所示。

?

　　坐標變換的步驟是:首先對圖像i (i=1,2,…,N)進行平移,使內螺紋外圓柱面中心與坐標原點重合;其次選擇某個標定系數進行比例變換,使N個圖像中的零件(以外圓半徑為準)具有相同的像素數;然后將圖像以原點為中心旋轉360°(N-i) /N;最后平移回到原始位置(采集位置)。可根據各個測球中心坐標在統一坐標系中的位置求得圓度誤差。

　　本文用解析方法確定各測球的分布中心(評定圓度的基準),使滾道圓度誤差的評定符合最小區域法。設某一螺距范圍內所有測球的球心坐標為(X0i, Y0i)(i=1,2,…,N),它們在端面上的理想分布應當在一個圓上。事實上,由于內螺紋滾道及測球的加工誤差及測量誤差,它們的分布是有誤差的。以N個測球球心坐標(X0i, Y0i)為擬合點,利用解析方法求出測球中心分布圓的圓心(X0*, Y0*),使其在評定圓度誤差時滿足最小區域原則。算法步驟如下:

?

　　=m+1,m+2,…,N+i-1),構造直線方程L′。

　　(2)分別求L與L′垂直平分線的交點Ow,以該點為圓心經過4個點做兩個圓,其半徑差即為最小區域法評定的4個點的圓度誤差。應時時判斷每一次計算的圓度誤差,滿足最小區域條件時即停止計算,此時的圓心Ow即為最小區域圓圓心(X0*,Y0*),否則轉步驟(3)繼續計算。

　　(3)i從1到N做循環,返回步驟1重復計算。上述循環計算中,從外到內的循環次序是i-g-m-k。滿足最小區域條件時,最小區域圓圓心至各測球中心距離中,至少各有兩個最大值Rmax及兩個最小值Rmin,且兩最大值坐標點連線與兩最小值坐標點連線的交點在最小圓內(最大值點與最小值點相互交替)。最小區域圓圓心(X0*, Y0*)至(X0i, Y0i)的最遠點(Xmax,Ymax)距離與最近點(Xmin,Ymin)距離之差即為圓度誤差,用下式表示:

?

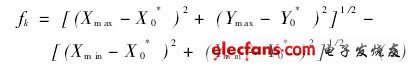
　　在內螺紋整個滾道內確定M個假想截面位置,重復測量每個位置的圓度誤差,取最大值作為內螺紋公稱直徑的圓度誤差。

　　4.2　滾道圓柱度誤差測量

　　在圓度誤差計算中,已經獲得了M個位置的測球分布中心(X0i*, Y0i*)(i=1,2,…,M)。同計算圓度采取的方法相同,將M個位置的數據統一在一個坐標中,共得到N×M個測球中心坐標,對它們進行圓度計算,可得到內螺紋公稱直徑圓柱度誤差。

　　4.3　滾道同軸度誤差測量

　　同軸度誤差是一種位置誤差,它是指被測軸線對基準軸線的變動量。在圓柱度誤差測量中,M個截面位置的測球分布中心(X0i*, Y0i*)是變化的,它的離散軌跡體現了被測軸線,而內螺紋外圓柱面的中心(Xb, Yb)是基準軸線。根據同軸度誤差的最小區域評定法則, (X0i*, Y0i*)與(Xb, Yb)距離的最大值的兩倍為內螺紋公稱直徑對其外徑的同軸度誤差。

　　4.4　滾道圓跳動誤差測量

　　在圓度誤差及圓柱度誤差測量中,測球球心坐標(X0i, Y0i)及螺母外圓柱面中心(Xb, Yb)已經求出,根據定義,分別計算(X0i, Y0i)至(Xb, Yb)的距離Ri,則該截面滾道圓跳動誤差為Rimax-Rimin。求解全部M個截面的圓跳動誤差,其最大值即為內螺紋滾道對基準(內螺紋外圓柱面軸線)的徑向圓跳動誤差。

　　4.5　實驗

　　本實驗依據提取的邊緣,應用開發軟件按前述幾何參數的計算方法,測量了內螺紋滾道的形位誤差。采集6個滾道截面進行測量(M=6),每個滾道截面采集12個圖像(N=12)。圖4為測球邊緣坐標和中心坐標(X0i, Y0i) (i=1,2,…,N)及其亞像素值(X0i', Y0i'),內螺紋外圓柱面的亞像素中心坐標(Xb, Yb)為(1026.349,751.128)(像素值)。計算出一個螺距范圍內12幅圖像的測球參數,以螺母外圓柱中心為基準經過旋轉、平移等變換統一到一個坐標系中,結果(像素值)如表1所示。

?

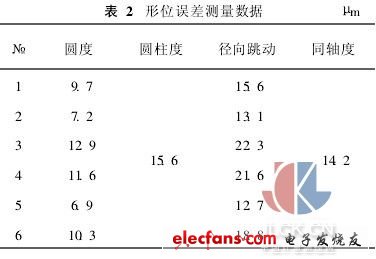
　　根據表1中數據,由整像素坐標按前述最小區域評定法求得圓度誤差為: f=0.731,最小區域圓圓心坐標為(1026.134,750.866);而根據亞像素坐標求得的圓度誤差為: f=0.449,最小區域圓圓心坐標為(1026.210,750.920)。該圖像的標定系數k=0.025 8,按整像素計算圓度誤差為0.731mm×0. 025 8= 0. 018 9mm,按亞像素計算圓度誤差為0. 449mm×0. 025 8=0. 0116mm。對應表1中的數據,求各個測球中心至螺母外徑中心之間的距離,其最大差值作為徑向圓跳動誤差值,計算結果為21. 6μm。最小區域圓圓心至螺母外徑中心之間距離的2倍為該截面滾道中心相對于基準軸線的同心度誤差,計算值為12. 9μm。6次亞像素測量結果見表2。

?

?

　　所測螺母形位誤差結果為:圓度誤差為0. 013mm,圓柱度誤差為0. 016 mm,徑向跳動誤差為0. 022 mm,同軸度誤差0. 014 mm。由文獻[2]可知,本文所測螺母的幾何尺寸及形位誤差項目中,除圓度誤差(公差為12μm)外,其余均符合技術要求。