常用四軸的兩種PID算法

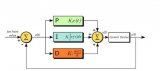
　　這里主要講解的PID算法屬于一種線性控制器，這種控制器被廣泛應用于四軸上。要控制四軸，顯而易見的是控制它的角度，那么最簡單，同時也是最容易想到的一種控制策略就是角度單環PID控制器，系統框圖如圖所示：

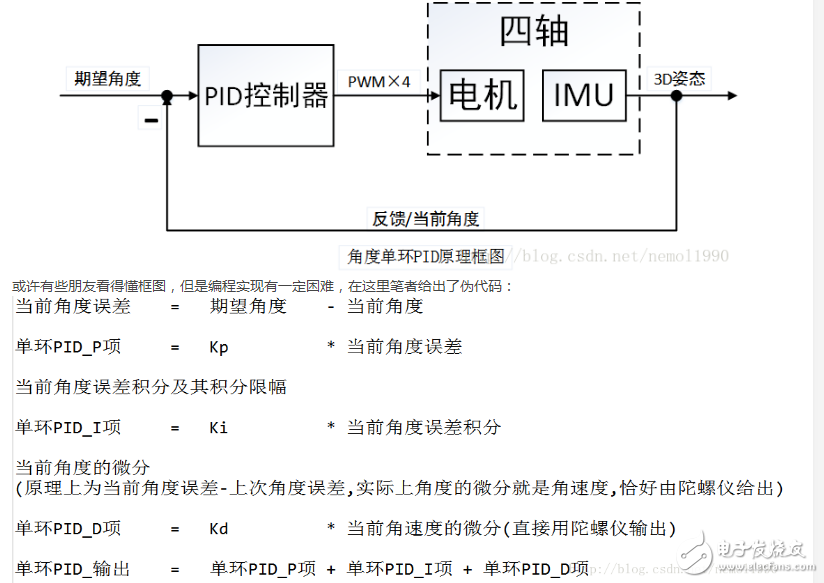
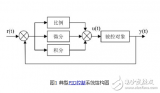
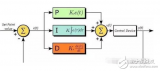
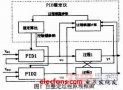
　　上述角度單環PID控制算法僅僅考慮了飛行器的角度信息，如果想增加飛行器的穩定性（增加阻尼）并提高它的控制品質，我們可以進一步的控制它的角速度，于是角度/角速度-串級PID控制算法應運而生。在這里，相信大多數朋友已經初步了解了角度單環PID的原理，但是依舊無法理解串級PID究竟有什么不同。其實很簡單：它就是兩個PID控制算法，只不過把他們串起來了（更精確的說是套起來）。那這么做有什么用？答案是，它增強了系統的抗干擾性（也就是增強穩定性），因為有兩個控制器控制飛行器，它會比單個控制器控制更多的變量，使得飛行器的適應能力更強。為了更為清晰的講解串級PID，這里筆者依舊畫出串級PID的原理框圖，如圖所示：

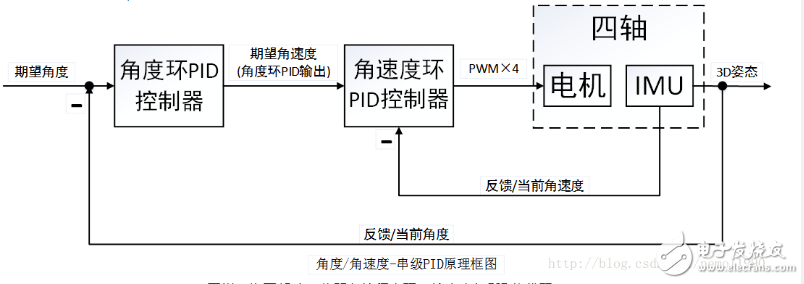
　　同樣，為了幫助一些朋友編程實現，給出串級PID偽代碼：

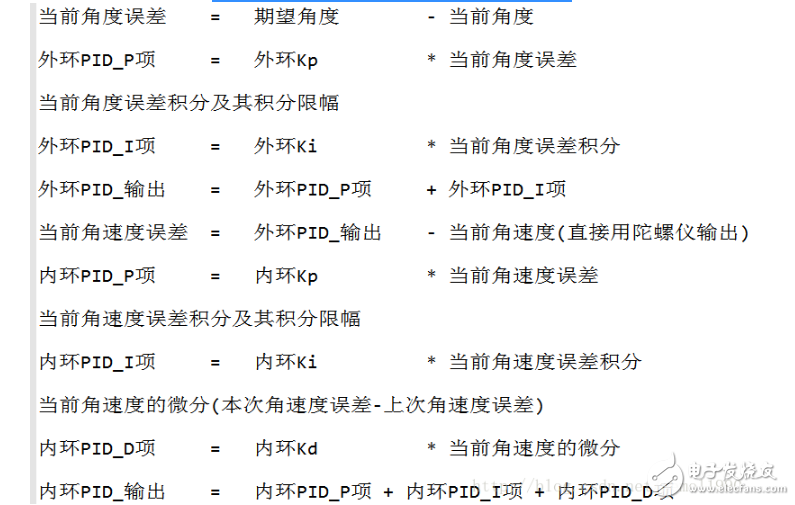
　　四軸專用PID參數整定方法及原理

　　使用PID的四軸會在飛行中震蕩，告訴大家為什么光使用PID并不能實現對四軸姿態‘足夠好’的控制。文章中還是涉及了不少自控原理和其他控制相關的姿勢，沒有一點底子的話確實會看著很困惑（不然那么些人花好幾年學控制還有什么意義？）。如果你只想知道結論的話，直接看文章開頭和結尾部分就好了

　　PID控制器是什么？

　　我想每一個看到這里的人都對PID的概念有了足夠的了解，我一遍遍嘰歪比例積分微分沒有任何意義。這里我只想說一些大家提的較少的‘重點’內容：

　　PID控制器是一個線性的控制器！從這里開始我們進入正題了，雖然若干年來PID已然成為了世界上使用最普遍的控制方法，也逐漸被人們神話到幾乎可以控制一切………………但是，從理論上來說，只有‘線性的，符合要求的’被控系統才能在PID控制下實現良好的控制效果。

　　所以說，我們首先第一步，要保證我們的被控系統在被PID控制的區域‘表現為’一個線性系統才行。于是這里有人會說了，現實中沒有哪個系統是線性的，自然，我們的四軸飛行器在大范圍內是一個非常典型的非線性系統（隨便按照理論推推模型就會出現漫天的三角函數），也就是說，我們‘僅’使用標準PID控制的話是不可能讓四軸從各個姿態回到目標狀態的過程都能保持穩定。于是這里出現我們使用PID時要注意的第一個問題：

　　我們的PID控制只能工作在四軸角度偏移不大的一個近似線性的區域內。這個區域沒有定論，不過你要是飛機偏了90°的話想用PID調回到水平狀態指定是非常危險的事情。PID的模型相關問題非常重要也比較費口舌，我們等下認真討論，現在要先說另一個非常重要的非線性問題：

　　要保證我的控制通道與電機的輸出力矩是線性的。如果我們的控制通道與電機輸出力矩都不是線性的的話，我們的PID控制就很難起作用了，節省時間不舉例子了，不明白的自行補腦吧，于是我這里要提醒大家的事情是：我們的航模電調調整的都是力矩而不是轉速（雖然它叫做電子調速器），這是我們的福音，因為大家知道，螺旋槳產生的升力與轉速的平方成正比，而角加速度與力矩成正比，正是因為我們的電調讓電機產生的升力與我們輸出的油門量成正比了我們才能使用PID控制器對四軸的姿態進行控制。這里可以看下我的四軸使用的四合一電調輸出的升力與油門的對應曲線：

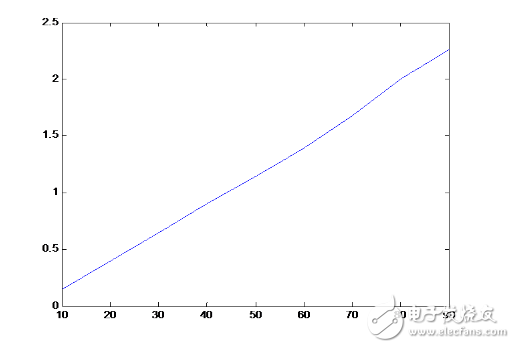
　　圖中橫坐標是輸出油門的百分比，縱坐標是四個電機產生的總拉力（單位暫定kg），可以看到，具有非常好的線性關系，所以我們可以使用PID對大四軸實現比較好的控制。于是我們首先發現了第一個問題，有人反映小四軸不好調參數，因為小四軸沒有專用的電子調速器，所以油門與輸出力矩并不是嚴格線性的（這里我沒有實踐過，請大家隨意批評指正），這時使用PID控制性能就會明顯下降，當你的電機輸出力矩與你的控制信號不是線性關系的時候，請先使用軟件補償的方法對油門做一下分段的線性仿射變化，再設計PID控制器。

　　不過對于大四軸而言貌似就不用那么麻煩了，那我們直接進入PID的控制模型環節。

　　PID控制器的數學模型

　　在標準的控制類書籍上PID算法是這么定義的：

　　這個公式是連續系統用的，我們單片機的控制是用不了的，我們的單片機使用的是離散的控制模型也叫0階保持器的離散系統，就是需要把上面的公式離散化，而這個離散化的過程我們使用的是后項差分法。首先把上面的積分傳遞函數轉化為連續的s域模型：

　　使用后向差分法可以得到s域到z域的映射關系：

　　于是可以得到：

　　這里特地給出了Kp Ki Kd這三個參數，這三個參數就是大家最常看到的那個離散的PID公式，也就是說你在這里既可以使用Kp Ti Td的參數來建模也可以使用Kp Ki Kd的參數來建模，到這里就總算是可以把我們的傳遞函數放在系統中用自控原理的相應工具來分析了。分析之前要先聲明一個事情，有人發現（比如在MWC和其他許多飛控中）用陀螺儀的輸出來當做PID中的微分項，會取得比標準PID更好的控制效果，乍一看這么做與用前后兩次歐拉角作差沒有區別（因為角速度整好就是角度的微分），控制效果不一樣就說不通了。

　　其實是這個樣子的，如果我們在程序中做了非常好的線程安全的處理并且控制頻率和姿態解算讀陀螺的頻率是一樣的的情況下二者確實是沒有任何差別的，但是大家的飛控都寫的非常簡單，姿態解算頻率都高于控制頻率，于是讀到的陀螺儀的數據并不是‘當前使用的姿態前一時刻’的數據而是‘后一時刻’的數據，這時候PID控制的微分部分就不再是‘后項差分’而是‘前向差分’了（這就是我前面要強調使用后項差分法的原因），那這個時候就尷尬了，我們不能全部使用前向差分模型來建模（因為積分還是使用的后向模型）兩邊分開用又會出現模型階次不匹配的問題，所以這時候是無法使用PID模型來考慮接下來的問題的，你使用的其實是兩個獨立的控制器并聯，一個是角度的PI控制器，而另一個是角速度的P控制器，二者采樣時間不一樣，于是得當做兩個獨立的控制回路調整參數，這是使用這種控制器時的參數調整方法。也就道出了為什么部分情況下使用角度微分和角速度控制效果不一樣的問題，這種方法固然是很好的（可以有效的降低振動），當然前提是你按照二者獨立控制的思路來設計參數。但是很不幸，大家都沒有這么做，依然是把整體作為PID控制器來考慮，那么，我只能說這是個近似的PID控制器了，手調固然可以（萬能的實驗調參啊）但是通過建模的方式算出優化的參數就不可能了。我們接下來看會怎樣：

　　從系統的零極點圖理解PID控制的原理

　　有了上面的PID傳遞函數的離散系統模型我們就可以開始下一步了，將上面的分式上下做因式分解可以得到系統的零極點，在自控原理中我們知道，系統的極點確定系統的穩定性情況，零點不影響系統穩定性，零點和極點共同決定系統的響應。這里說的有些模糊，在現代控制理論中會提到一種控制器叫零極點配置控制器，能更好的闡述零點的作用：系統中的零點可以用來與系統中的不穩定（或者不想要）的極點對消來設計出理想的控制器（數學上），工程中我們考慮的是讓零點與我們不想要的極點盡可能的靠近，就能削弱這個不想要的極點對系統的影響。下面我們用極點配置的方法來設計PID控制器，這里提前聲明我們使用的并不是最標準的閉環極點配置方法，因為我們的PID控制器只有兩個零點可以配置（如果使用PI控制器的話就只有一個零點可以自由配置了）而且還多了一個臨界穩定的極點，反饋又使用的是單位負反饋……極大的限制了極點配置的自由度，于是我們為了簡單起見僅從開環部分進行極點配置，這么做有許多不嚴謹的地方，但是會簡化許多工程上的應用（在做自適應PID控制器的時候會用到完整的極點配置方法，到那里就會發現是多么復雜的一件事兒了……）。

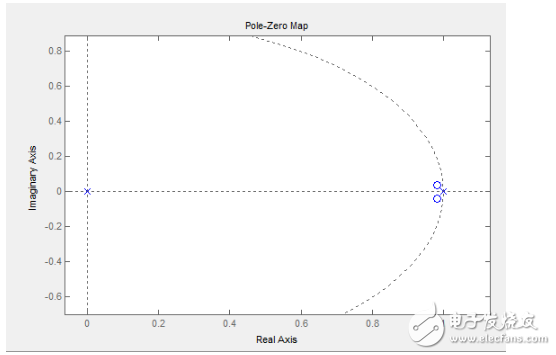
　　上圖是PID控制器開環部分（就是上面推導的數學模型）常見的零極點分布情況，有兩個固定在（0，0）和（1，0）位置的極點，兩個對稱分布的零點（手調參數時很難出現兩個零點都在實軸上的情況而且我們也不希望那樣），這兩個零點的位置是可調的，微分時間常數Td主管零點位置的左右移（注意是‘主管’，也就是說對虛軸的位置還是有影響的），常數越大越靠右（也就是說臨界穩定極點的影響越弱，抗噪聲性能越好但到達0誤差的穩態也就越困難，因為這個臨界穩定的極點是在閉環系統中讓系統到達穩態0誤差的關鍵但很影響穩定性），積分常數Ti越大零點越靠近實軸，Ti在實際控制中的作用不好說明，留在后面再說，但是到這里大家也就看出我為什么要使用標準的Kp Ti Td參數而不是Kp Ki Kd參數了，因為使用這種參數時Kp對開環系統的穩定性（注意僅指開環系統）沒有影響，我們就可以降低系統對這個參數的敏感性而主要考慮另外兩個參數就好。大家在手調參數的看到的圖形和這個都應該沒有多少區別

　　接下來我們看一下我們被控系統的數學模型：

　　被控系統的小范圍線性化模型

　　正如我前面所述，想要分析PID的控制性能必須得得到被控系統的線性近似模型（非線性系統下的分析工具沒個正經能用的），這里大家可以通過動力學建模得到系統的非線性模型（像幾乎所有的碩士博士論文那樣）再泰勒展開，但是這樣做往往得到的模型跟實際情況差異太大以至于沒有參考價值，這里我推薦使用系統辨識的方法來得到系統的線性模型，因為這么做如果能做到正確的辨識的話還能得到系統的誤差模型，于是現在在控制界很流行，只是實際用的時候就發現難度頗高，盡管有許多現成的工具但是依然特別難掌握，也難怪很多熱會把這個當做是看家本領，作者在這方面也算是連皮毛都沒摸全，不敢亂講，這里就為了解釋PID方便直接把我的大四軸辨識出來的Pitch軸模型拿出來當做例子來講了：

　　畫出來的系統階躍響應是這個樣子的：

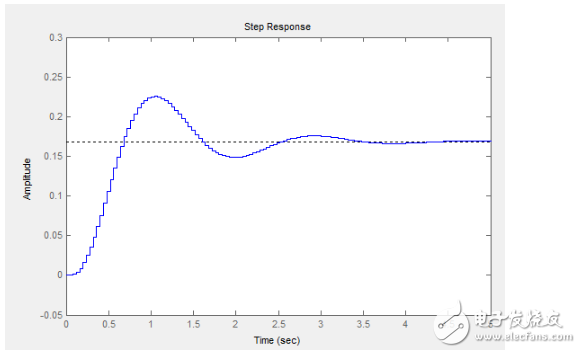
　　檢驗系統建模的相似程度就靠這個了，給我的飛機一個階躍信號反映出來的情況和這個確實差不多。關鍵是下面，它的零極點分布情況：

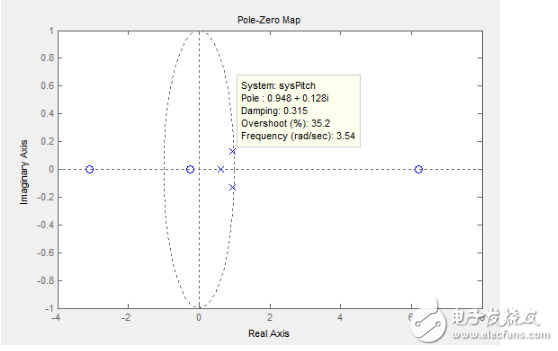
　　可以看到辨識出來的結果又兩個很靠近不穩定邊界的主導極點（氣泡框那里）表現明顯的零點又和這幾個極點8桿子打不著，如果我們消滅那兩個主導極點，我們的四軸理論上就可以控制的非常完美了，眾所周知，主導極點越靠近0則系統穩定性越好，那么按照極點配置的方法（當然我這里指的還是開環的極點配置），那么我們接下來開始看用這種建模的方法怎么實現PID參數的配置：

　　用極點配置PID實現對系統的控制

　　那么按照上面的介紹我們來嘗試消除這兩個主導極點，前面說過，PID模型中兩個對稱零點的位置是可以任意調整的，不用計算，直接手試出如下的參數：

　　那么得到的開環零極點圖是這樣的：

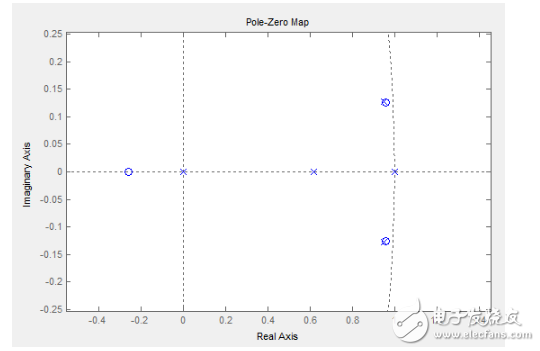
　　那么閉環響應是這個樣子的：

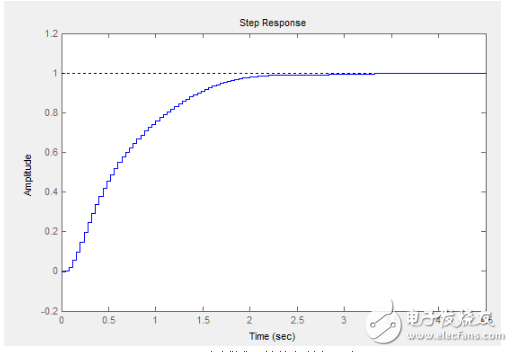
　　看著很漂亮啊，我們加大Kp到4試試，其他參數都不變

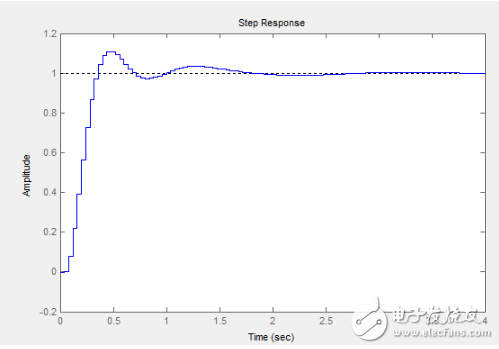
　　喲，完美嘛，0.5s即可到達穩態，0穩態誤差，超調量也不過10%而已，相當的理想，而且從這里可以看出使用Kp Ti Td參數的優勢：隨意調整Kp，可以提高系統性能而且對閉環穩定性幾乎沒有影響，甚至對開環系統的穩定性完全沒有影響，我想，這也就是MWC飛控用Kp（角速度的）作為動態參數的原因。那么好吧，令人沮喪的部分終于要來了，把這個參數燒到飛控里面，運行，哇塞，不錯哦，不動搖桿它平衡的很好，那我們遙控下……我擦，越抖越大，控制不住了，翻了，打到人了，鮮血汩汩而出……………………

　　這是為什么呢？來看下我們這時的開環系統階躍響應：

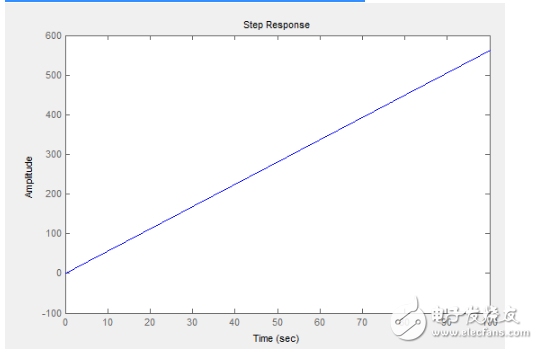
　　咦？怎么是一條直線呢？沒錯，它就是這樣一個不穩定的狀態，在我們高興的做極點配置的時候，忘記了PID控制器本身還會引入一個臨界穩定的極點，這個極點帶來的好處0穩態誤差，但是卻對噪聲非常敏感，也就是說，如果我們的飛機在氣流平穩的地方飛行，飛機的電機性能又極佳，建模也準，最關鍵的，是姿態解算的精度又出奇的高的話，用這種方法得到的PID參數肯定是非常完美的。但是現實總是殘酷的，具體為什么會對噪聲這么敏感應該可以從系統的噪聲辨識模型中得到解釋，但是很遺憾到文章這里我并沒有對噪聲進行建模，有興趣的可以嘗試下。

　　這里就是使用PID控制的弊端了，它只提供了兩個零點用來對極點進行抑制，但是又同時引入了一個不穩定的極點，不得已，我們只能讓零點從那兩個極點上向那個臨界穩定的極點移動，企圖用兩個零點來牽制三個極點，這自然沒辦法達到良好的控制效果，但也就成了沒有辦法的辦法了……大家在搜索PID參數整定方法的時候一定都聽說過Ziegler-Nichols整定法則，這幾乎是PID基于模型的參數整定唯一的方法了，但是為什么沒人把這個如此著名的整定方法（這里指第一方法）應用在四軸的PID整定中呢？因為使用該法則有個鐵打的前提：控制對象中既不能包含積分器，又不包含主導共軛復數極點，也就是說階躍響應應該是一個S型…………………………很不幸，我們的四軸這兩條都占了……積分器是在從角速度到角度轉換的過程中，在與其他好多極點的共同作用中最終在我們的參數辨識中表現為了那兩個討厭的共軛復數極點，重新看一遍我的解釋流程，就明白為什么不能用Ziegler-Nichols整定第一法則了，也就是為什么光用PID不能達到足夠好的控制效果。

　　那么，既然非要用PID飛又既然缺少極點的情況下我們只能讓零點右移，這么做的理由也是可以從另一個方面來佐證的：

　　調過PID的都知道增加微分可以提高系統的抗噪性能，減小積分會減小噪聲積累（這里指Ki增加而不是Ti）反映到零點的移動中剛好就是零點向右側的（1，0）點移動。所以可以得知，我們經過權衡能得到的PID最佳的控制參數的零點應該是落在了開環主導極點和（1，0）點連線所在的那一片區域內了，那么我們對PID的分析是否到此就結束了呢？顯然沒有，我還沒有論證為什么大家在數年的總結中會得到“先調P，再調D，最后調I就能飛了”的實驗整定方法能夠湊效，并且還要提出個理論指導實踐的方法來……

　　自控原理的書上有提到“串聯響應頻率校正”的設計方法，但是該方法屢試都不爽，有興趣可以從這個方向走走，說不定能為我們的四軸PID控制器設計找到一條出路。

　　之前我曾說過，用Kp Ti Td型的參數設計的PID控制器穩定性對Kp并不敏感，那么我們是不是可以利用這點來優化我們的控制器設計呢？答案是肯定的。我們先來看下按照上面的‘向右看齊’參數調整方法會發生什么：

　　我們隨便選一個在連線上的點作為參數查看它的開環零極點和閉環階躍響應（這里Kp去1）：

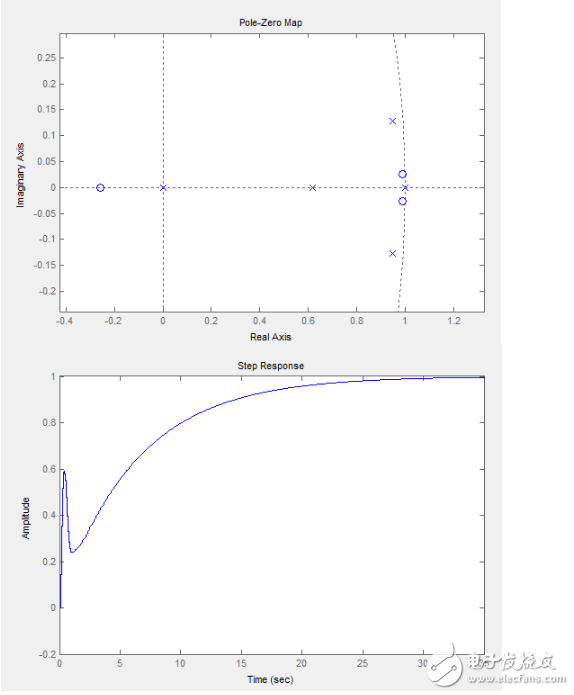
　　可以看到，積分的效果明顯減弱了，系統先在0.幾秒的時候迅速的達到了穩態（0.3左右）然后在以后漫長的時間內在積分作用的影響下以指數逼近最終的穩態1，大家看著這個圖應該很快就想到該怎么做了，就是增大Kp，讓系統的‘第一個’穩態在1附件，那問題就解決了，不錯，我們這里把Kp設為4（不設置為3是為了等下驗證另一個東西）：

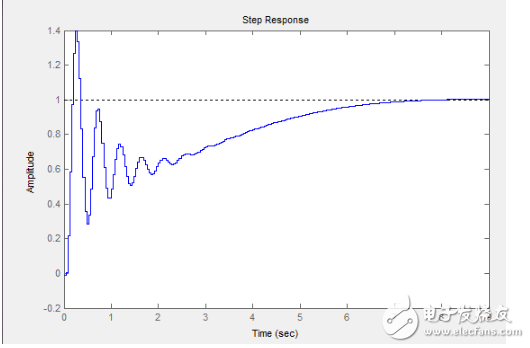
　　瞧，這個很丑的怪物出現了，比剛才好了不少，而且你最終得到的PID控制器輸出效果會和這個差不了許多（之所以在視頻上看不出來是因為人很少會從0----Pitch角0°突然給飛機一個1----Pitch角57°）另外要說的是為什么我用了4依然沒有讓它的第一步就穩定到1，這是因為閉環降低了系統總增益，但是這里給再高的增益會讓系統不穩定，原因就在下面了：

　　為了更直觀的說明不穩定的原因，這里要用Bode圖來看一下系統閉環的頻域響應：

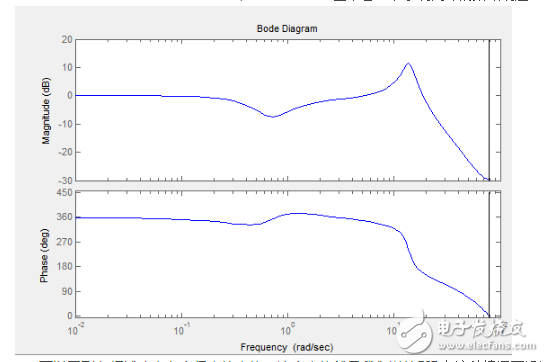
　　可以看到在頻域響應有個很尖的尖峰，這個尖峰就是我們說的PID在這種情況下沒法達到優良控制性能的關鍵，你會發現，使用純PID控制的飛控，都會在空中來回抖動，頻率基本是固定的，就是這個尖峰的緣故，尤其當Pitch軸和Roll軸使用同樣的控制參數的時候，抖動會疊加，你經常會看到視頻里用純PID控制的四軸在兩個控制軸交界的方向上抖啊抖抖啊抖抖啊抖抖啊抖…………于是這里就是我們需要用實驗來權衡的地方，這個尖峰通過減小Kp的值可以得到一定的抑制，也可以讓零點向左少許移動，二者都會延長到達穩態的時間，比較明智的做法是保證有足夠的響應速度的前提下適當減小增益，畢竟在PID沒法很好的完成控制任務的情況下，人的操作就顯得非常重要了。這里給出我使用的一組PID參數：

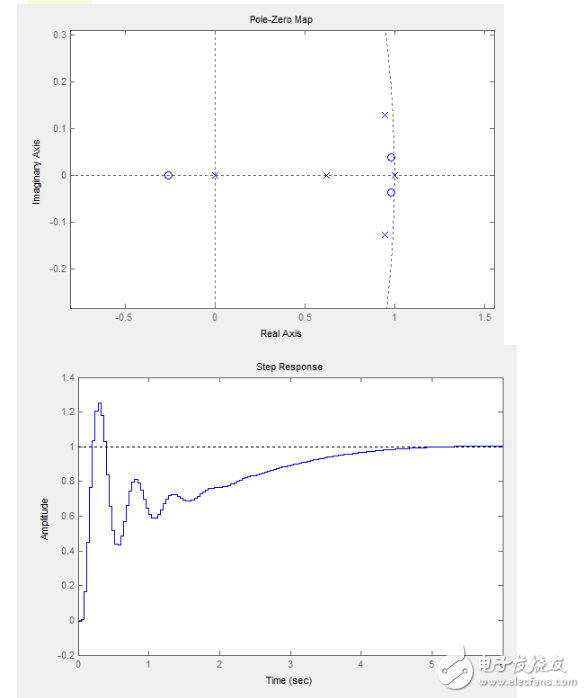
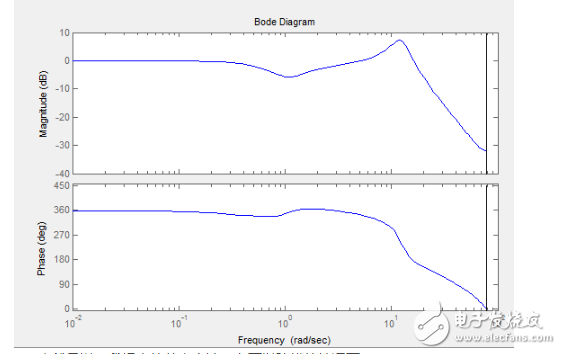
　　也就是說，我提出的整定方法，在可以建模的情況下：

　　①建立被控系統的模型

　　②根據上述的原則確定PID的開環0點應該出現的區域（就是在那個連線上）

　　③給一個開環情況下穩態誤差較小的Kp

　　④看著階躍響應微調Ti和Td使得在保證Td足夠大的情況下超調量較小且積分效果打到穩態的時間又足夠的長（2~3s以上依據個人口味）

　　⑤最后看著Bode圖適當減小增益Kp

　　⑥回頭再檢查下階躍響應是否滿足心意就完事兒了

　　看到這兒，不知道有多少人會和我一樣苦苦的一笑（這TM繁瑣的步驟有意思嗎？），這么做確實是一件非常不值得的事情，只是如我這般不服氣的孩子憑著一股刨根問底的沖勁花了2個月用自己的方式來調PID的真實記錄而已，好了，現在再來介紹不建模的情況下怎么通過試驗整定四軸的PID參數

　　其實試驗方法整定PID參數使用的依然是Ziegler-Nichols整定法則，不過這次使用的是第二法則，而且做完以后要按照我接下來給的步驟微調

　　鑒于該整定法則在阿莫上沒有人提過（至少我沒有找到），這里先貼上完整的Ziegler-Nichols整定第二法則：

　　首先，該法則使用Ti Td的參數形式（現在更理解為什么要用Ti Td參數格式了吧？）先僅使用Kp進行控制（取Ti為無窮大，比如32767，取Td為0，等價于Ki=0 Kd=0）從0開始慢慢增大Kp直到第一次出現臨界穩定的情況記錄下當前的Kp值計作Kc……

　　這里暫停一下，注意這里的臨界穩定的含義，調參時請用一根圓桿子橫穿四軸的重心，這個時候四軸會在桿子上等幅擺動，這個時候可不是臨界穩定啊！四軸風扇油門推到很大的時候氣流是會給一定旋轉的阻力的，如果你Kp調到沒過5它就等幅震蕩了那絕對是不對的，要把油門推到飛機平時剛好起飛的位置（既桿子與飛機接觸面基本不受力）。另外就是等幅震蕩并不是說你把它放在那兒它慢慢岳震越大了，而是你給個階躍響應它按照那個幅度等幅震蕩，比如你用手輕輕撥了一下，它就在那個范圍等幅震蕩了。這個點很精確，多一小點就發散，少一小點就能慢慢停下來，比如我的四軸測完是11.6

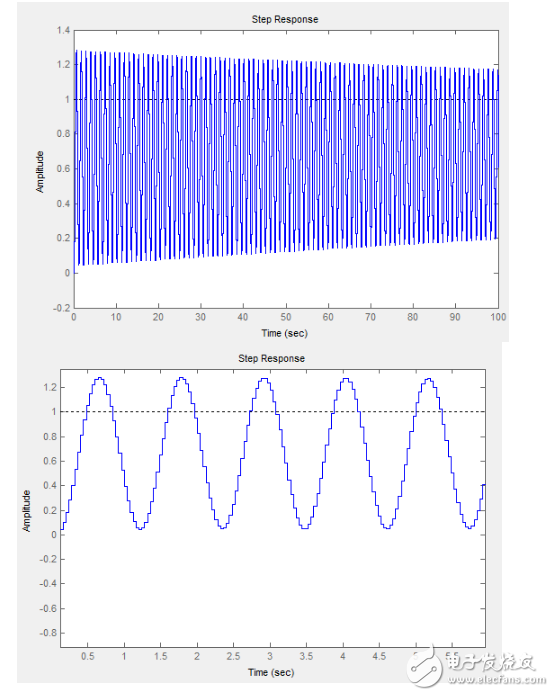
　　…………繼續，則這時你需要測量它震蕩一個周期的時間（單位為s）計做Pc，那我們就可以得到用Ziegler-Nichols整定第二法則得到的PID參數：

　　Kp = 0.6Kc

　　Ti = 0.5Pc

　　Td = 0.125Pc

　　我們看下這個參數的階躍響應和開環零極點：

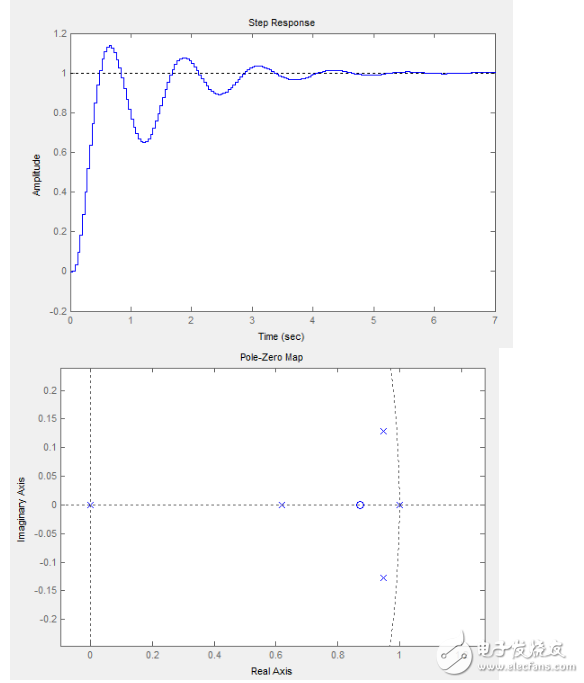
　　你會發現它只有一個零點，其實這并不是一個零點，而是兩個零點重合了，但是你把這個參數燒到四軸上以后出現的情況和我前面的極點配置方法得到的情況非常相像，因為它的微分系數太小了，抵抗擾動的能力很弱，這里要說明為什么他要用一個重合的零點，大家在做控制的時候很少遇到這種震蕩特性很強的系統，大家遇到的基本都是一階的系統（階躍函數表現為單調增到達穩態），這時候用這種無虛部的零點可以讓超調量最小。

　　那么，也許有很多人跟我一樣，剛開始調PID的時候兩次調到這里，一次是應為震蕩點沒選對，Kc小了太多導致控制完全不起作用于是放棄了。第二次調對了Kc但是發現穩態效果很差，在Ki Kd的參數下折騰了好久越調越爛最終把這個方法放棄了。我估計到現在壇子里沒見到這個整定方法很有可能就是這個原因吧。

　　那么好了，我這里要告訴你到了這一步該怎么繼續調，不要動Kp和Ti，增大Td直到你覺得快速用手轉動你的四軸的時候有了足夠的阻力（注意是快速轉動的過程中，而不是你壓著它不動的時候的阻力），這時候你的四軸應該就已經調好了，想進一步微調就是你自己的事情了，讓我們來看下這個時候系統是什么樣子的，我們僅給這時的Td參數加上0.5（取個比較整的數而已，要是取1就更明顯了）

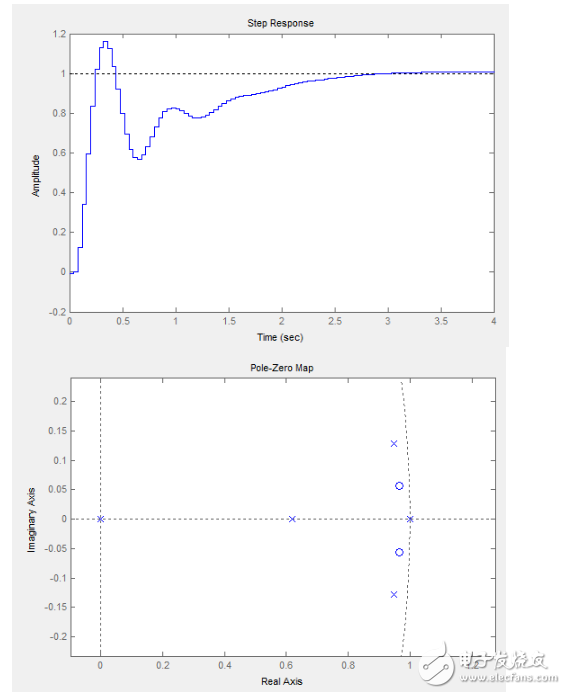
　　有沒有發現和我前面得到的參數非常接近？看著這個圖，結合前面我提到的內容，又有什么感悟呢？

　　維基百科上有個詞條《齊格勒－尼科爾斯方法》，里面用的是Ki Kd的參數形式，需要用我前面提到的Ki Kd和Ti Td的轉換關系轉換一下。

　　總結：PID該怎么調，我們該注意什么

　　①先要保證電機的輸出是線性的，微型四軸等沒有電調的最好先對電機的油門行程和供電電壓進行矯正，保證對電機的控制輸入和電機輸出的力矩程線性關系。

　　②嚴格注意自己控制程序中的每一步是否有線程安全的問題，不要讓四軸的一次控制運算中使用了不是同一時間的狀態測量值。

　　③用陀螺作為微分項能減少姿態解算誤差帶來的干擾，但要小心有可能會破壞了PID的控制模型導致控制效果變壞。

　　④作者強烈建議你使用Kp Ti Td的PID參數形式。

　　⑤記住Kp Ti Td參數變化對系統產生的影響是什么樣的。

　　⑥注意調參的時候你是怎么固定你的四軸的。

　　⑦選擇我上面提到的我的兩種調參方法的一種整定參數。

　　⑧不要相信僅用PID能調出完美的四軸控制器，PID僅僅能讓你的四軸飛起來而已，更不要相信增量式PID能在四軸的姿態控制中有所作為，牛逼的開源不開源四軸都不僅僅使用了PID控制器。

　　⑨不要手賤報控制專業

　　這里附上MATLAB的仿真代碼

　　［plain］ view plain copy%% lynx的四軸飛行器PID調試模型

　　clc，clear

　　%被控線性模型

　　TfPitchNum = ［-0.00004584 0.0001312 0.0009171 0.000228］;

　　TfPitchDen = ［1 -2.514 2.087 -0.5657］;

　　sysPitch = tf（TfPitchNum，TfPitchDen，0.04）; %重新構造無噪聲輸入的模型

　　%ltiview（sysPitch）

　　sysPitchZpk = zpk（sysPitch）;

　　%使用標準PID參數的柿子，這個是一個可用的參數

　　Kp = 6.5;

　　Ti = 0.8;

　　Td = 1.1;

　　% %臨界穩定增益

　　% Kp = 11.6;

　　% Ti = 1000;

　　% Td = 0;

　　% %齊格勒-尼克爾思整定方法

　　% Kp = 11.6*0.6;

　　% Ti = 0.5*1.1;

　　% Td = 0.125*1.1+0.5;

　　Ts = 0.04

　　Ki = Kp*Ts/Ti; %0.3

　　Kd = Kp*Td/Ts; %17

　　p2 = Kd;

　　p1 = -Kp-2*p2;

　　p0 = Kp+Ki+p2;

　　ControlSys1Num = ［p0 p1 p2］;

　　ControlSys1Den = ［1 -1 0］;

　　ControlSys1 = tf（ControlSys1Num，ControlSys1Den，0.04）;

　　SysOpen = series（ControlSys1，sysPitchZpk）;

　　SysSum = feedback（SysOpen，1）

　　ltiview（SysSum）

　　ltiview（SysOpen）

　　%ltiview（ControlSys1）

　　tf（ControlSys1）