Curvelet變換是基于傅里葉變換和小波變換的一種改進,其特點是有高度的各向異性,具有良好表達圖形沿邊緣的信息的能力,對于恢復形狀的沿邊緣的主要結構和抑制周邊噪聲有其特有優勢。
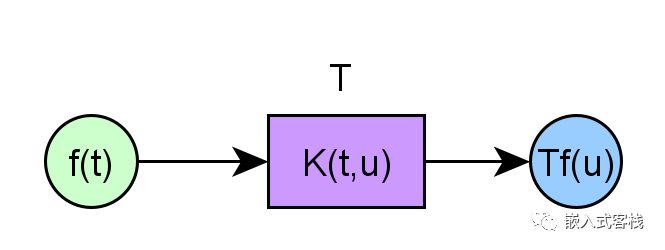
其過程為
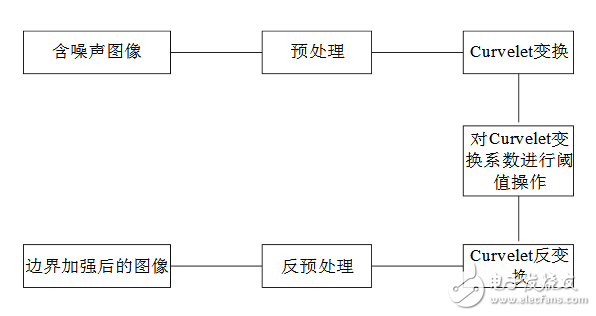
這和傳統的DFT及小波變換的處理過程類似,把圖表中的curvelet換成DFT和wavelet就可以了。
Curvelet變換是最近圖像處理較新的一種多尺度幾何變換算法。其發展歷程在短短十年間:
1999年,Candès和Donoho在Ridgelet變換的基礎上提出了連續曲波(Curvelet)變換——第一代Curvelet變換中的Curvelet99。
2002年,Strack、Candès和Donoho提出了第一代Curvelet變換中的Curvelet02。
2002年,Candès等人提出了第二代Curvelet變換。
2005年,Candès提出了兩種基于第二代Curvelet變換理論的快速離散實現方法:
1)非均勻空間抽樣的二維FFT算法(Unequally-Spaced Fast Fourier Transform,USFFT);
2)Wrap算法(Wrapping-Based Transform)
與小波變換類似,Curvelet變換同樣有其對應公式。Curvelet系數可由下式得到,即信號與小波函數內積:
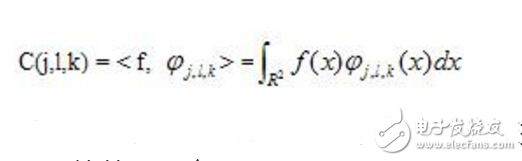
這里j表示尺度,l表示方向,k表示位移。變換的推導以及原理是個十分復雜的過程,這需要有相當強的數學功底。
Curvelet變換原理
Curvelet 變換通過對Radon 域內的每一個投影軸作一維小波分析,并由局部脊波分析得到多尺度結構。設參量θ是常數,平移量1是變量,脊波系數R,(a,b,θ)為


然后對每個分塊用式(1,2)進行脊波分析。上面每步均可逆,經過逆變換可得重建圖像。
通過Radon域的多角度投影,Curvelet變換明顯加強了目標邊界。同時由于Curvelet變換是多尺度脊波變換的子集,它可以用投影切片定理來實現:一幅n×n的圖像可表達成2n條徑向線的積分結果,對每條線的投影數據計算一維小波變換,就得到脊波系數。這樣的Curvelet變換冗余因子達到16J+1。由于經典算法中分塊的徑向抽樣角度恒定,直角坐標與極坐標的轉換將導致在同一塊內數據的非均勻抽樣,當塊中心附近的抽樣值滿足奈奎斯特抽樣定理要求時,在塊的邊界部分將出現欠抽樣;而當塊邊界部分滿足抽樣定理要求時,塊中心部分數據將會過抽樣,而且塊的尺寸越大,非均勻抽樣的影響就越明顯。因此,在原算法中盡管離散Curvelet變換的實現較簡單,但是為了無失真地重構圖像,保證塊邊界周圍的抽樣值足夠多,它在塊的中心部分實施了過抽樣,因此耗時和冗余度也相應增大。
 電子發燒友App
電子發燒友App














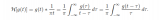













評論