Curvelet變換是基于傅里葉變換和小波變換的一種改進,其特點是有高度的各向異性,具有良好表達圖形沿邊緣的信息的能力,對于恢復形狀的沿邊緣的主要結構和抑制周邊噪聲有其特有優勢。
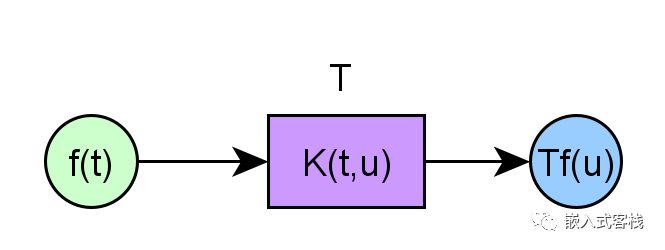
其過程為
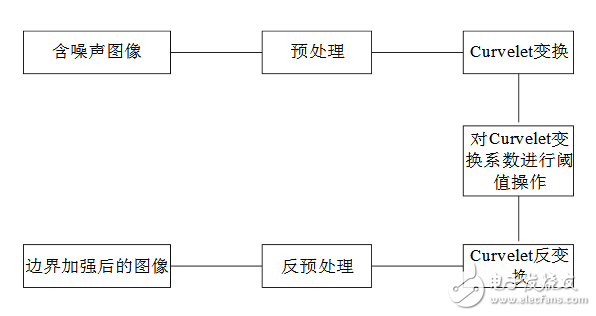
這和傳統的DFT及小波變換的處理過程類似,把圖表中的curvelet換成DFT和wavelet就可以了。
Curvelet變換是最近圖像處理較新的一種多尺度幾何變換算法。其發展歷程在短短十年間:
1999年,Candès和Donoho在Ridgelet變換的基礎上提出了連續曲波(Curvelet)變換——第一代Curvelet變換中的Curvelet99。
2002年,Strack、Candès和Donoho提出了第一代Curvelet變換中的Curvelet02。
2002年,Candès等人提出了第二代Curvelet變換。
2005年,Candès提出了兩種基于第二代Curvelet變換理論的快速離散實現方法:
1)非均勻空間抽樣的二維FFT算法(Unequally-Spaced Fast Fourier Transform,USFFT);
2)Wrap算法(Wrapping-Based Transform)
與小波變換類似,Curvelet變換同樣有其對應公式。Curvelet系數可由下式得到,即信號與小波函數內積:
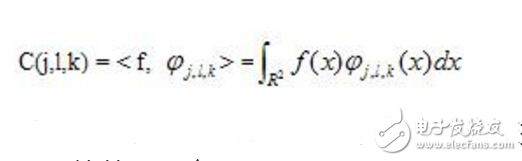
這里j表示尺度,l表示方向,k表示位移。變換的推導以及原理是個十分復雜的過程,這需要有相當強的數學功底。
Curvelet變換原理
Curvelet 變換通過對Radon 域內的每一個投影軸作一維小波分析,并由局部脊波分析得到多尺度結構。設參量θ是常數,平移量1是變量,脊波系數R,(a,b,θ)為


然后對每個分塊用式(1,2)進行脊波分析。上面每步均可逆,經過逆變換可得重建圖像。
通過Radon域的多角度投影,Curvelet變換明顯加強了目標邊界。同時由于Curvelet變換是多尺度脊波變換的子集,它可以用投影切片定理來實現:一幅n×n的圖像可表達成2n條徑向線的積分結果,對每條線的投影數據計算一維小波變換,就得到脊波系數。這樣的Curvelet變換冗余因子達到16J+1。由于經典算法中分塊的徑向抽樣角度恒定,直角坐標與極坐標的轉換將導致在同一塊內數據的非均勻抽樣,當塊中心附近的抽樣值滿足奈奎斯特抽樣定理要求時,在塊的邊界部分將出現欠抽樣;而當塊邊界部分滿足抽樣定理要求時,塊中心部分數據將會過抽樣,而且塊的尺寸越大,非均勻抽樣的影響就越明顯。因此,在原算法中盡管離散Curvelet變換的實現較簡單,但是為了無失真地重構圖像,保證塊邊界周圍的抽樣值足夠多,它在塊的中心部分實施了過抽樣,因此耗時和冗余度也相應增大。
下面是對Curvelet變換的理解:
在時間域:Curvelet變換可以看做是一個橢圓以內積形式依次覆蓋整個矩陣(指要變換的矩陣),這個圖在很多地方都出現過。就我個人的理解詳細解釋下。
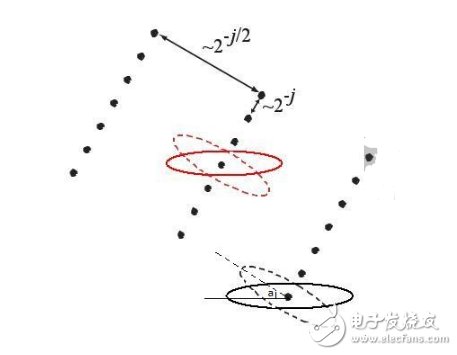
這里的橢圓就是Curvelet變換的窗口,相當于小波變換的基函數。其長軸與短軸關系為平方關系,其窗口大小視尺度j而定。與二維小波變換最大的優勢在于Curvelet變換具有方向性。就是在尺度j下,橢圓做完整個矩陣的內積后(即依次覆蓋完整個矩陣),可得到一組系數。然后將橢圓進行旋轉適當的角度a再與矩陣做內積得到a角度的Curvelet系數。這樣將橢圓進行多次旋轉,每旋轉一個角度就能得到尺度j一個方向的系數矩陣。在尺度j下做L次旋轉,那么尺度j下就產生L個角度的系數矩陣。做完尺度j了接下來做尺度j+1下所有角度,方法同上。
如一幅圖像上有一段弧,橢圓長軸沿著弧方向做覆蓋內積得到的系數就大。這樣就適合做圖像邊緣檢測。
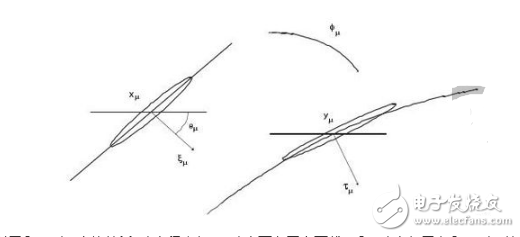
對于Curvelet變換的Matlab程序包curvlab可在網上下載。Curvlab包里有Curvelet的快速離散算法的Matlab程序和C++程序。
將其添加在Matlab里面:File -》 set path
Add Folder 添加好curvlab里相關*. M文件的路徑。
這時在Matlab里面使用Curvelet的快速變換及反變換函數:
fdct_usfft()
ifdct_usfft()
fdct_wrapping()
ifdct_wrapping()
在Matlab中Curvelet變換后返回的是一個cell矩陣。這個矩陣裝著各個尺度、各個方向的系數值。
C= fdct_usfft(***);
C{j}表示一個cell矩陣,裝著尺度j上所有方向的系數。
C{j}{l}就表示是一個二維矩陣,表示尺度j,方向l上的所有系數,
一般尺度越高,其對應的都是高頻系數。
curvelet matlab示例代碼理解
1. fdct_wrapping
function C = fdct_wrapping(x, is_real, finest, nbscales, nbangles_coarse)
% fdct_wrapping.m - Fast Discrete Curvelet Transform via wedge wrapping - Version 1.0
%
% Inputs
% x M-by-N matrix 輸入為MxN的矩陣
%
% Optional Inputs
% is_real Type of the transform 轉化的類型
% 0: complex-valued curvelets 復數值的曲波變化
% 1: real-valued curvelets 實數值的曲波變化
% [default set to 0] 默認設置為0
% finest Chooses one of two possibilities for the coefficients at the
% finest level: 選擇一種表示方式計算最優級的系數
% 1: curvelets 曲波變化
% 2: wavelets 小波變化
% [default set to 2] 默認設置為2
% nbscales number of scales including the coarsest wavelet level
% 包含最粗小波級在內的伸縮數
% [default set to ceil(log2(min(M,N)) - 3)]
% nbangles_coarse
% number of angles at the 2nd coarsest level, minimum 8,
% 第二粗糙級的角度數,最小為8
% must be a multiple of 4. [default set to 16]
% 必須為4的倍數,默認為16
% Outputs
% C Cell array of curvelet coefficients.
% C{j}{l}(k1,k2) is the coefficient at
% - scale j: integer, from finest to coarsest scale,
% 從最佳尺度到最粗尺度
% - angle l: integer, starts at the top-left corner and
% increases clockwise,
% 從左上角開始順時針增長
% - position k1,k2: both integers, size varies with j
% and l.
% If is_real is 1, there are two types of curvelets,
% ‘cosine’ and ‘sine’。 For a given scale j, the ‘cosine’
% coefficients are stored in the first two quadrants (low
% values of l), the ‘sine’ coefficients in the last two
% quadrants (high values of l)。
%
% See also ifdct_wrapping.m, fdct_wrapping_param.m
%
% By Laurent Demanet, 200412345678910111213141516171819202122232425262728293031323334353637383940414243
2. DCT基本示例代碼理解
% fdct_wrapping_demo_basic.m -- Displays a curvelet both in the spatial and frequency domains.
m = 1024;
n = 1024;
X = zeros(m,n);
%forward curvelet transform
disp(‘Take curvelet transform: fdct_wrapping’);
tic; C = fdct_wrapping(X,0,2,8,64); toc; %tic toc配合使用測量程序運行時間
%specify one curvelet
s = 7; %從1開始增大,空間域變細,頻率域變粗
w = 10;%從1(左上角)開始增大,空間域順時針旋轉,與笛卡爾corona相對應
[A,B] = size(C{s}{w});%尺度為s,方向為w,的矩陣大小
a = ceil((A+1)/2);
b = ceil((B+1)/5);
C{s}{w}(a,b) = 1; %該尺度、方向中心位置元素設置為1
%adjoint curvelet transform
disp(‘Take adjoint curvelet transform: ifdct_wrapping’);
tic; Y = ifdct_wrapping(C,0); toc;%進行反曲波變化,得到空間域圖像
%display the curvelet
F = ifftshift(fft2(fftshift(Y)));
subplot(1,2,1); colormap gray; imagesc(real(Y)); axis(‘image’); 。。。
title(‘a curvelet: spatial viewpoint’);
subplot(1,2,2); colormap gray; imagesc(abs(F)); axis(‘image’); 。。。
title(‘a curvelet: frequency viewpoint’);
%get parameters
[SX,SY,FX,FY,NX,NY] = fdct_wrapping_param(C);
 電子發燒友App
電子發燒友App














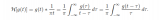













評論