從數學的角度,提供一個形象有趣的解釋。理解傅里葉變換的鑰匙是理解基♂,它能讓你重新認識世界。
1. 什么是基?
假設一個科研所有四個所長(一正三副),四個所長各司其職,把整個科研所的事物管理得井井有條。這四個所長,少一個,單位的工作無法順利展開,多一個礙手礙腳事倍功半,他們四人一道就組成了科研所的一個“基”。
一個單位的基可能不是唯一的,四個人換換位置工作也能展開,調走一個人再換一個人來頂替,單位亦可以正常運轉,但是4這個數是不能變化的(數學語言:空間的維數固定不變)。
總結:一組基,就是足夠能描述、表達某類事物的最少的一小撮元素們。
2. 基只有一種形式嗎?
我們把科研所的日常事務換成感情,把四個所長換成語言字典重新來敘述。
假設你愛上了一個人,需要向她表達感情。這時就需要一套表達感情的工具——語言。如果使用漢語,你可以說“我愛你”,如果使用英文,你可以說“I love you”。漢語的所有詞匯構成了一個集合,英語的所有詞匯也構成了一個集合,它們都可以描述感情、感覺、事物和知識,它們是兩套不同的描述系統,分別有自己的基。
總結:描述事物的基可以有很多套。
3. 如何構造一組基?
漢語的詞匯量很大,有很多重復意義的詞,比如我愛你就可以重新表述為:“俺愛你”,“我愛儂”,“我想和你困覺”等等。我們把漢語詞匯中所有同意的詞只保留一個(數學語言:使線性無關),留下來的詞匯量較少的詞典就是漢語的一個基,里面的每一個詞被稱作基函數。它的特點是:所有漢語能描述的思想都可以用從這個較小的詞匯本中挑出的一些詞匯(基函數)經過精心安排(加權相加)來描述,并且只有一種描述方式(數學語言:若基固定,則對應系數/坐標確定),因為我們已經去掉了所有冗余的、近似的詞匯,因此不存在一個事物在一個基下有兩種不同表示法存在。
總結:一套基中的元素很多,足夠描述事物,只要從中挑出一些你需要的,按某種方式組合在一起即可,一套基中的元素很少,以至于這種描述事物的方法是唯一的。
4. 不同基之間有什么聯系?
給定兩個不同的語言,給出兩個不同語言的小字典(兩組基),我們都可以分別用唯一的方式表達同一思想(函數、點),這兩種表示法之間可以相互轉換(數學語言:坐標變換)。“I love you”和“我愛你”可以相互轉化。
總結:給定一個基,我們就可以用這組基表達事物,也可以用它來翻譯用其他基描述的事物,不同基下的表示可以相互轉換。
5. 什么是傅里葉變換?
大家還記得三角函數sin和cos嗎,就是那種波浪形狀的函數,一個波浪的的寬度可以是不同的,既可以像跳大繩一樣寬,也可以像電爐絲一樣窄(數學語言:頻率不同)。把這些三角函數放到一起組成一個字典,就恰好是連續函數的一組基:任何一個連續函數,都可以唯一表示成一群三角函數相疊加。然而每個三角函數的分量有輕有重,相加的時候有的要拉高點,有的要壓低點,有的干脆不用(數學語言:加權系數不同)。到底是哪些三角函數呢,各個三角函數的分量如何呢?找到它們的過程,被稱為傅里葉變換。
舉幾個例子:
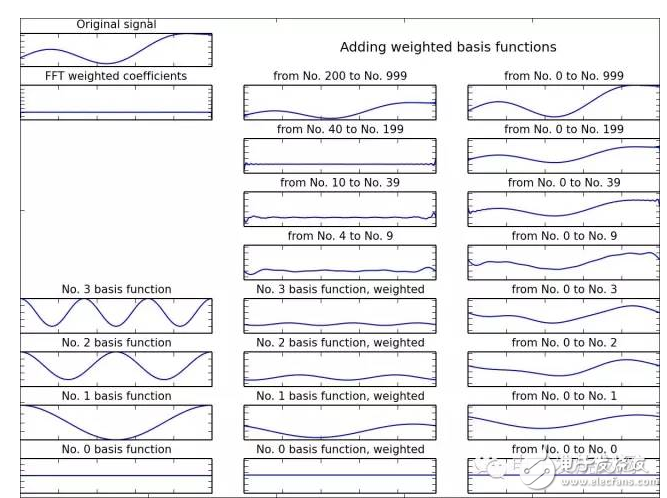
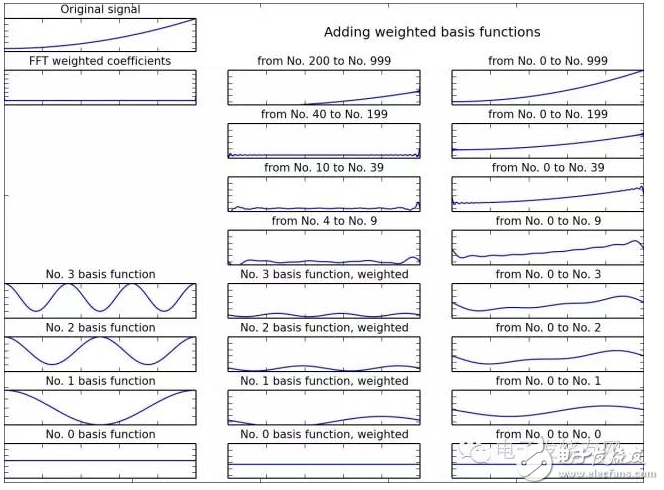
下面兩個圖,左上角是某個函數(信號)的樣子,它等于1000個震蕩的三角函數相加,中間一列從下往上是這1000個三角函數中第0、1、2、3個,以及中間6、30、160、800個相加的樣子,注意好幾個三角函數加在一起就不再像是三角函數了。右邊一列從下往上是把這些三角函數疊加在一起,1000個加在一起和原函數完全一樣,但是前40個三角函數函數加在一起和原函數已經很相似了。
從這幾個例子可以看出,把一系列震蕩的三角函數按照傅里葉系數(權值)進行縮放再加起來,大概40個三角函數加到一起,就和原來的函數長得差不多了,無論原來的那個函數長的有多么奇特。因此我們說:螞蟻也能撼大樹,三角函數多了加到一起,多奇怪的連續函數我長的都能和你是一個樣。
總結:給你一個函數,找到它的傅里葉變換,就是找到一堆系數,每一個系數對應一個不同頻率的三角函數,這些三角函數分別按各自的系數改變振幅(數學語言:確定坐標),然后疊加在一起,恰好就與原來那個函數相等。
因此,四個處長是一組基,能維持一個單位的運轉,處理各種問題;
一套簡化的漢語詞典是一組基,什么樣的情感它都能找到唯一的表達語句;
一堆三角函數是一組基,什么樣的連續函數都可以用一大堆三角函數疊加獲得,找到這種表示的過程叫做傅里葉變換。
6. 傅里葉變換有什么用?
擺弄一系列三角函數,讓這個多點那個少點,有一個酷炫的名字,叫“頻域處理”,
你去了美國,不知道白宮怎么走,你問翻譯:白宮怎么走?
翻譯跑到街上問美國人:Where is the White House? 這叫傅里葉變換。
美國路人說:“go straight and turn right”。這叫頻域處理。
翻譯聽完給你說:直走,右拐就到了。這叫逆傅里葉變換。
總結:傅里葉變換的作用,就是把一個函數或者信號在三角函數基下轉化為一堆系數,擺弄這些系數、實現一定功能有時比直接擺弄原信號方便,最后再做個逆傅里葉變換,信號就得到了某種處理。
7. 傅里葉變換與壓縮、簡化表示
從第5小節我們知道了基變換的一個用處:壓縮信號。原始信號需要用1000個點來表示,但是其實只需要40個三角函數系數就可以表示出大概。大家天天都會遇到的JPG圖片就是干這個事的,一張800*600的彩色照片,如果保存成非壓縮的BMP圖像格式,需要占據1.4M存儲空間,如果保存成JPG格式,大概50K就夠了。JPG能壓縮得這么厲害,訣竅就在于它用了一組特別的基(小波基),使用特別少的基函數就可以把原始圖像表示得八九不離十,在這里頻域處理就是把絕大多數基函數前面的系數直接置0。為什么能這么干呢?因為小波基有很強的表達能力,我們總能選取極少的幾個小波基函數就能拼出任意一個給定的圖像的大概,然后即使拋棄剩下那些大量邊角料,也不太會對視覺效果造成什么影響。
說到這里你肯定一頭霧水,咱們再來做個類比來說說基的壓縮能力。想象這樣一個故事:女主角出生在孤兒院,和男主角相遇但是被拋棄,生下一個女兒,她后來做了個變性手術,穿越回到過去和還是女兒身的自己啪啪啪,帶著女兒再次穿越到自己被收養時的孤兒院把嬰兒拋棄在那。
如果你缺乏語言能力,比如你是一條狗,你怎樣讓另一條狗理解孤兒院、男、女、啪啪啪、拋棄、愛情這些真實世界中極度復雜的概念?你能做的最好的重述就是雇一男一女和一個時光機,把故事演一遍,對方還不一定能懂。語言能夠在短短的一段話里就描述出這一個復雜的故事,因為它拋棄了大量細節,只保留最重要的信息:如果說真實世界每一個對象(物體、故事、情感)是一個函數,那么語言就是一組新的基,在這組基下,每一個基函數(詞匯)都具有高強的描述能力,復雜的對象可以用聊聊幾筆進行描述、壓縮、傳遞,讓人類能夠高效地交流,快速地學習。
一個海岸有多少粒沙子?多少滴海水?一幅800*600像素的圖像就能捕獲你在海邊嬉戲的靚影,只用了48萬個基函數,如果你用JPG格式存儲,調動的基函數還會更少。普通非壓縮位圖數字圖像的基函數長的都一樣:在一顆像素是白色(1),在其他所有像素都是黑色(0)——一個基就是一根孤零零的矩形棍子,其對應的系數就是對應像素的顏色值,真彩色的系數有約1600萬種。
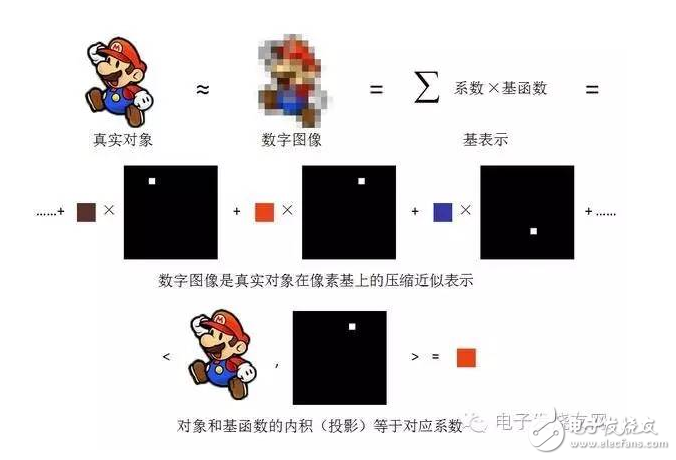
傅里葉變換和這幅圖中的變換非常類似,只不過基函數不是一顆像素,而是震蕩的三角函數。所有三角函數Asin(ax+b)也可以由一個三角函數 sin(x)通過改變頻率a,相位b和振幅A來獲得,這種情況很有意思:一組基中所有的基函數都是由一個基函數進過簡單地平移、拉伸或改變振幅獲得。它的實質是另一種意義上的壓縮:我們用一個基函數(數學語言:母函數)通過簡單形變來生成其他基函數,再用它們一起表示更復雜的元素。我們不需要拉來一頭牛一只羊來表示這里有一頭牛一只羊,我們只需要用許多個基本元素,每一個都差不多,就能近似表示復雜的場景。這一思想的一個有趣的應用是游戲 Minecraft,在這里基函數是一些等大立方體塊,把它們拼在一起則組成了復雜世界的近似。
這個圖和上面用40個三角函數近似一維信號、一堆像素近似二維物體是完全類似的,這里是用立方體近似三維世界。同樣是對真實世界的近似描述,我們可以用一堆抽象詞匯、用像素、用立方體塊,也可以用三角函數形狀的“塊”,使用彼此近似但略微不同的基函數,我們就可以對無比復雜的真實世界的對象進行壓縮、近似。三角函數基唯一的奇怪之處在于它是震蕩的,看著不萌。
壓縮的缺點是無法反向恢復,可以從一幅圖像變換到另一幅,但是不能從一幅圖像恢復真實世界。但是沒人想捧著真實世界,人們需要的恰恰是對真實世界的高度凝練地表示。
8. 頻域處理能干啥?
如果你不懂英文,一個妙齡少女對你說:Hi. I love you. Are you free tonight?你會回復她:姑娘你能不能不要說鳥語?滾回美帝玩泥巴吧。如果你懂英語,就會發現姑娘說的東西其實是有某種意義的,可以進一步處理。
在某些領域,傅里葉變換后的系數非常有用,我們前面已經舉了傅里葉變換能夠壓縮數據的例子,下面再舉幾個其他例子。為了顯示方便,舉一個二維的例子,見下圖:
原始圖像中含有噪聲,因為噪聲往往是細小的雪花點,屬于圖像高頻分量,因此我們把圖像首先做傅里葉變換,然后把變換后的三角函數前的系數中屬于高頻的部分全部去掉(置0),然后再做逆傅里葉變換,我們發現圖像中的細節(噪聲點)減少了。這就是頻率域去噪的基本原理。
在音頻處理中,不同人對于同一個音節發出的聲音,其傅里葉變換后的系數是不同的,并且可能每個人的模式是穩定的,就像指紋一樣,那么傅里葉變換后的系數就可以來識別、合成某個人的聲音,把某個人的發音中的某些系數進行調整,就變成了另一個人發音;所有人對于不同詞匯的發音的傅里葉變換系數也可能具有某些固定模式,利用這些模式可以發展聲音的理解技術,比如Siri。現在政府監督電話敏感詞,再也不是找接線員一個個聽了,而是用電腦自動監聽,如果發現某人的通訊中敏感詞頻率較高,再派專人處理。
9. 還有哪些基我們可能聽過,但是不曾認識到?
多項式基:多項式多了,啥稀奇古怪的函數都能表示,不信你試試泰勒展開式有多好用就知道了。
小波基:傅里葉基(三角函數)的改進,可以進行局部控制。
B-樣條基:多項式基的改進,可以進行局部控制,畫家畫畫用的就是這東西。
一幅800*600的圖像,我們既可以認為它是一幅抽象的圖像,也可以認為它是一個由800*600個基函數(一個基函數是某一顆像素值為1,其他所有像素值為0的圖像)進行加權相加獲得的一個坐標表示。
 電子發燒友App
電子發燒友App














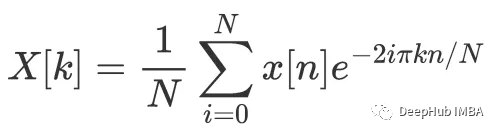










評論